优化 ｜ 线性规划和整数规划的若干建模技巧

编者按

大家在对实际问题按照线性规划建模时，有没有因为一些特殊的变量或者约束而束手无策。例如目标函数是个求最大最小值问题，变量带绝对值符号，约束条件只能二选一。这篇文章介绍的建模技巧，让你轻松地将上述棘手难题转换为线性规划问题。

文章申明
文章作者：liuao0910(运筹学分享交流)
责任编辑：蓝
文章由『运筹OR帷幄』授权转载发布，如需转载请在公众号后台获取转载须知

1. 线性规划问题建模的重要性

现实生活中，有很多问题可以描述成优化问题，然后利用运筹优化的知识加以解决。它们通常遵循以下流程：

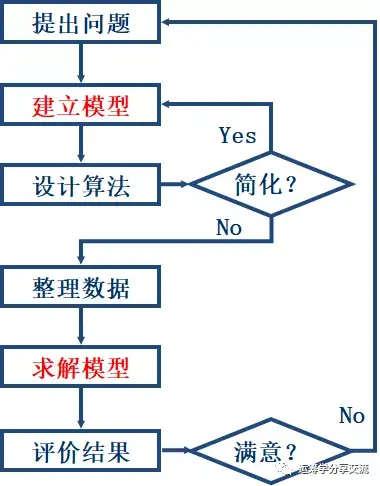
可以看出，比较核心的两个步骤是：建模(modeling)和求解(solve)。

对于现在有很多成熟的软件或者工具包，可以求解线性规划问题。比如，lingo, cplex, gurobi, glpk，lpsolve, scip，matlab optimization toolbox等。

实际问题成千上万万，它们的约束、目标等各不相同。如何对实际问题建模，并将它归结为一个线性规划问题，是应用线性规划求解问题时最重要，往往也是最困难的一步。问题建模是否合理，很大程度上会影响到后续的模型求解过程。

但是，受限于实际问题特征、建模经验、建模技巧等因素，我们在对问题建立初步模型之后，目标函数和约束条件往往包含一些特殊约束或者特殊变量：

• 含有绝对值。比如，LASSO回归是L1范数回归，目标函数包含绝对值
  

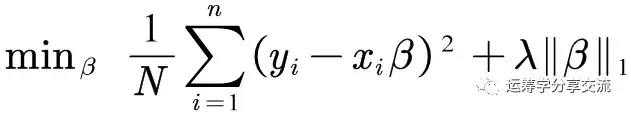
• 含有最大(最小)值。比如，风险决策涉及的最小机会损失准则( min-max)，也称最小最大后悔准则。
  

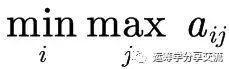
• 二选一约束。比如，同时生产两种产品A和B，产量分别为x和y，要么采用高负荷生产，满足2x+3y<=100，要么采用低负荷生产，x+y <=50。

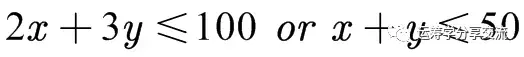
• 其他特殊约束或变量。

对于上述含有特殊约束或者特殊变量的问题，尽管看起来不是线性规划问题，但是通过一些建模技巧，可以将它们转化成线性规划问题。

2. 含有绝对值的建模

比如，有如下规划问题：

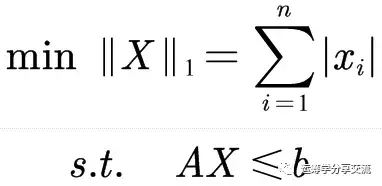
为了将其转化为线性规划问题，引入两个新的非负向量u和v，满足以下条件：

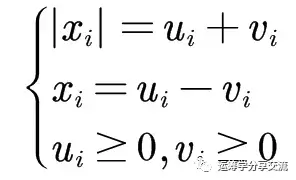
上述规划问题就转化为如下线性规划问题：

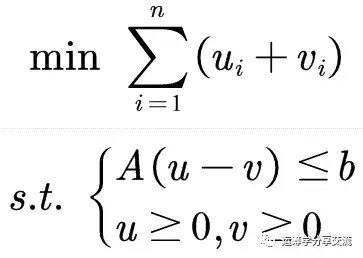
3. 含有最大(最小)值的建模

比如，有如下规划问题：

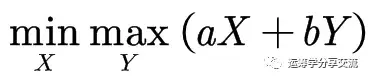
为了将其转化为线性规划问题，引入新的变量u，满足以下条件：

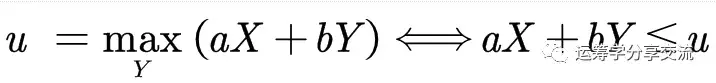
上述规划问题就转化为如下线性规划问题：

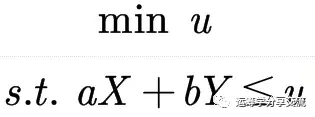
4. 二选一约束的建模

比如，有如下约束：

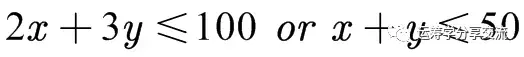
该约束实际上是一个二选一约束，为了将其转换为线性约束。引入一个0-1变量z和一个充分大的数M(大M法):

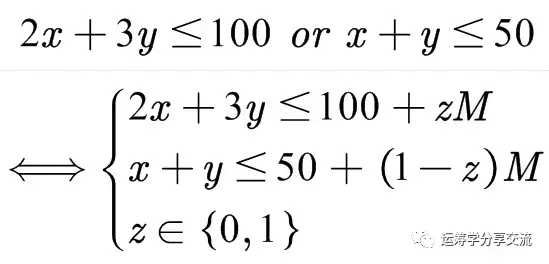
5.多选多约束的建模

比如，有如下3个约束，要满足其中2个约束：

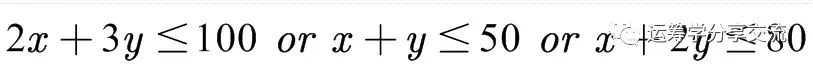
该约束实际上是一个3选2约束，为了将其转换为线性约束，引入3个0-1变量z和一个充分大的数M(大M法):

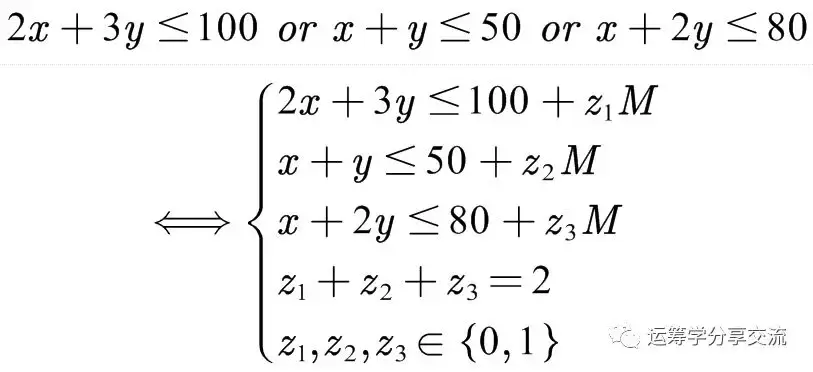
6. 固定成本约束的建模

在库存问题中，通常考虑订货的固定成本和可变成本。就是说，只要订货x>0，就有一个固定成本k，和可变成本cx，它的成本函数就是：

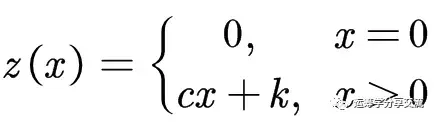
该约束实际上是一个二选一约束，为了将其转换为线性约束。引入一个0-1变量y和一个充分大的数M(大M法):

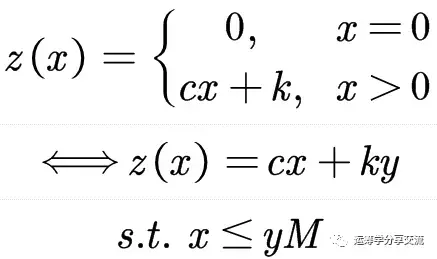
7. 分段线性函数的建模

比如，在现实生活中，购买商品的数量越多，它的单价会有折扣。在数学中，它的一个成本或者利润函数就可以表示成如下的分段线性函数：

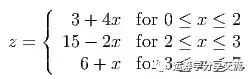
对于分段线性函数，可以通过引入SOS2约束(a special order set (SOS) constraint of type 2)，将其转换为线性规划。以下是一种比较通用的建模技巧。

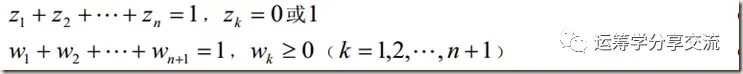
事实上，像CPLEX、LP_SOLVE等solver，已经支持直接对分段线性函数建模，不需要建模人员将其进行线性转换。

参考资料

[1]Special Ordered Sets (SOS)

http://lpsolve.sourceforge.net/5.1/SOS.htm

[2]Modeling piecewise linear functions

http://homepages.rpi.edu/~mitchj/handouts/ piecewise/

[3]Matlab随笔之分段线性函数化为线性规划

https://blog.csdn.net/weixin_34269583/article/details/86014299

[4]Piecewise Linearity in CPLEX

https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.1/ilog.odms.cplex.h

相关文章推荐

更多运筹学学习方法可参考如下文章：

点击蓝色标题，即可阅读《主编推荐 | 千里之行，始于足下，运筹学学习路线规划与入门法则精选》

其他

【学界】运筹学之线性规划

加入『运筹OR帷幄』知识星球的好处

• 中国你能说出名字的几乎所有大厂（资深）算法工程师入驻
• 欧美数家大厂（资深）软件工程师入驻
• 以上所有公司独家内推机会
• 简历修改指导
• 面试咨询， 模拟面试
• 得到一对一指导、解答工作中的疑惑
• 多家Offer选择指导
• 以面试题为学习资料学习真正的算法干货，从小白变成大咖
• 不定期的线上、线下交流会和聚会,拓展人脉。

欢迎关注『运筹OR帷幄』公众号

点击查看『运筹OR帷幄』志愿者招募介绍及加入方式：