基于Jaya学习的独立光伏、风机和电池系统的最佳容量优化

《1. 引言》

1. 引言

传统能源发电使用石油、天然气和煤炭等化石燃料资源，这些资源会随着消耗而枯竭[1]，并造成环境污染和全球变暖。例如，化石燃料的使用和燃烧会导致有毒气体的排放，从而导致环境问题，给生物健康带来巨大风险[2]。二氧化碳（CO₂）约占人为产生的温室气体排放量的77% [3]。这些因素通过破坏气候而导致环境中有毒气体的排放。因此，开发更环保、经济、清洁、取之不尽的新能源生产方式是当前最重要的任务。可再生能源（renewable energy source, RES）是一种新兴能源并被广泛应用，其利用各种自然资源发电，包括太阳能、风能、地热能、水力发电和其他自然补充能源[4]。在可再生能源中，风力涡轮机（wind turbine, WT）和光伏发电（photovoltaic, PV）是最主要、最鼓舞人心的技术，并且被国际社会视为可以满足电力消费者负荷需求的发电技术[5]。

与其他能源相比，由太阳能和风能系统组成的可再生能源受到了更多的关注，因为它们倾向于减少全球 CO₂排放[6,7]。然而，根据自然条件，这些资源是不可预测的和间歇性的。因此，可再生能源的可靠性是一个需要以最低成本解决的主要问题。为了解决环境问题，在能源生产中需要考虑可再生能源。可再生能源有两种实现方式：并网（grid-connected, GC）和独立（stand-alone, SA）模式。在GC模式下，可再生能源将产生的电力注入电力公用事业网络，而在SA模式下，可再生能源直接为用户的电力负荷供电[8]。

在GC系统中，用户直接连接到公用电网。如果 RES的电力不足，用户可以从公用电网获得电力并满足其负荷需求。因此，GC系统不存在可靠性问题。SA系统引入了不可靠性问题，因为用户仅依赖于RES产生的电力，并且没有与电网系统连接。此外，在SA环境中使用单个RES会导致较大的能量变化。这种影响会导致能源不匹配的情况发生，即发电容量不能满足用户的负荷需求。为了克服可再生能源的不可靠性和相关挑战，参考文献[9]采用了混合可再生能源系统（hybrid renewable energy system, HRES）和储能系统（energy storage system, ESS）来满足用户的负荷需求。太阳能和风能的互补特性与HRES以及ESS备份结合在一起。由电池、燃料电池（fuel cell, FC）和其他技术组成的ESS被用来解决压力期间（即RES产生的能量小于所需负载）的能量不足问题。因此，由HRES和ESS一起供电的解决方案被认为比单个RES更可持续、更可靠[10]。

HRES的主要问题是确定单个组件的最佳容量，包括WT、PV和电池。战略决策需要优化规模，如进行可行性研究、初始资本投资或成本估算。以可维持系统可靠性的最小年度总成本（total annual cost, TAC），来确定准确合适的HRES组件容量的方法称为单元容量[11]。 RES的不可靠性可以通过扩大系统组件容量来解决；然而，这样做会增加系统成本。另一方面，系统组件容量过小会导致供电中断（loss of supply, LOS）问题，即 RES产生的能量小于用电设备的负荷。因此，在减少 TAC的情况下，关系着系统组件确切数量的HRES的最佳单元容量至关重要[12]。

基于软件的工具、形式化技术和元启发式算法通常用于确定RES的单元容量。可再生能源混合优化模型（hybrid optimization model for electric renewable, HOMER）是一种基于软件的工具，用于能源优化、敏感性分析和规划。Mamaghani等[13]建议使用PV-WT-柴油发电机HRES为哥伦比亚3个偏远的离网村庄供电，他们对成本进行了技术经济可行性分析，并对二氧化碳进行了环境评价。HOMER软件工具用于技术经济性HRES 分析，以满足每天13 048 kW、估计峰值为1185 kW的平均负荷需求 [14]。就净现值（net present cost, NPC）和二氧化碳排放量而言，PV-WT-柴油-电池系统每年可提供的最佳结果分别为1.715×10⁷ 美元和2.571 131× 10⁶ kg。相比之下，单台柴油发电机产生的电能每年可产生2.109×10⁷ 美元的净现值和5 .432 244 ×10⁶ kg的二氧化碳排放。Karmaker等[15]使用PV-生物质-电池系统对孟加拉国的电动汽车供电进行环境和经济可行性评估。通过HOMER Pro软件得出的结果显示，与基于电网的电动汽车充电相比，使用该系统可减少34.68%的二氧化碳排放量，每月可节省12~18美元。参考文献中使用的HOMER软件[13–15]存在一些局限性，它不能进行多目标优化，只支持基于NPC最小化的单目标函数。此外， HOMER不支持小时内的基本可变性，并且对于大型设计点需要大量的计算时间。

考虑到HOMER软件的局限性，它的工作方式类似于参考文献[16–18]中通过混合整数线性规划（mixed-integer linear programming, MILP）求解RES的最佳单元容量。Ren等[16]考虑了一个GC方案，其中住宅能源需求通过PV-FC-电池系统得到满足。作者提出了一个多目标函数来同时降低年成本和二氧化碳排放量，通过 MILP描述这个问题，并考虑将能源卖回电网。结果表明，电池有助于提高经济效益，而PV则是一种环境友好的解决方案。然而，MILP是一种形式化的技术，存在一些局限性。MILP技术对解决方案空间执行了完整搜索，以找到确切的解决方案。然而，这种方法不适用于随机环境，并且受大型设计点容量问题的困扰。

其他研究建议使用元启发式算法，包括人工蜂群优化（artificial bee swarm optimization, ABSO）[19]、遗传算法（genetic algorithm, GA）[20–22]、和声搜索（harmony search, HS）[23,24]和粒子群优化（particle swarm optimization, PSO）[25–27]等，与其他方法相比，这些算法更具连续性和高效性[28]。然而，诸如HS、PSO、GA和 ABSO等技术需要特定于算法的参数才能发挥作用。例如，HS算法使用和声记忆、基音调整和即兴合成的取值概率，而PSO算法需要具有惯性权重值的认知和社会参数。GA算法需要一个选择算子以及交叉和变异概率。同样，ABSO不能在没有初始化和调整算法特定参数的情况下执行，这些参数包括“雇佣蜂”“侦察蜂”和“观察蜂”的数值。遗传算法和蚁群优化等算法也需要对算法的特定参数进行性能调整，以获得最佳结果。如果调整不当，特定于算法的参数可能造成局部最优解或增加计算时间。

元启发式算法如PSO、ABSO和GA，不仅需要特定于算法的参数，而且需要对其参数进行性能调整，以获得最优解决方案。这些算法的性能主要取决于这些参数的选择、校准和性能调整。任何参数的微小变化都可能影响算法的整体性能，并可能导致计算时间增加或陷入局部最优状态。因此，文献中已经提出了一些算法，包括Jaya [29]、基于教学的优化（teaching–learning-based optimization, TLBO）[30]和改进的TLBO[31]，这些算法不需要任何特定的算法参数。此外，这些算法的功能只依赖于某些通用控制参数，如世代数和种群规模。

本文通过Jaya、TLBO及其混合算法JLBO来解决 HRES的单元容量问题。我们考虑使用PV-WT-混合动力电池系统，它比其他使用柴油发电机的混合动力系统更环保、更具成本效益。下面列出的贡献是我们之前工作的延伸[32]：

（1）PV-WT-电池系统的各种组件均采用信息丰富的 HRES模型进行制定和阐述。

（2）在非算法特定方法的激励下，提出了Jaya和 TLBO算法来寻找HRES及其组件的最佳数量，以降低 SA环境下用户的年电费。

（3）结合Jaya算法和TLBO算法的学习阶段，提出了一种混合算法JLBO，用于优化解空间的搜索。

（4）使用用户提供的各种最大允许供电损失率（maximum allowable loss of power supply probability, LPSPmax）的数值来考虑系统的可靠性。

本文各部分安排如下：第2节描述了所提出的系统模型、容量确定公式和基于一些约束的目标函数；第3 节中给出了求解方法；第4节中给出并讨论了仿真结果；第5节提供了结论和未来的工作展望。

《2. 系统模型和容量公式》

2. 系统模型和容量公式

本部分包括系统模型以及RES和TAC建模的公式。

《2.1. 提出的系统模型》

2.1. 提出的系统模型

图1显示了PV-WT-电池HRES的典型系统模型。提出的系统模型由单直流（direct current, DC）总线体系结构组成。总线连接到双RES，包括光伏板和WT。太阳能和风能系统的间歇性会导致RES产生非线性且不可预测的输出功率。因此，在SA模式下使用单个RES将导致能量变化。故而，本文使用包含太阳能和风能系统的HRES与ESS。ESS由电池组成，这些电池存放在电池组中。按照惯例，ESS使用深循环铅酸电池。

《图1》

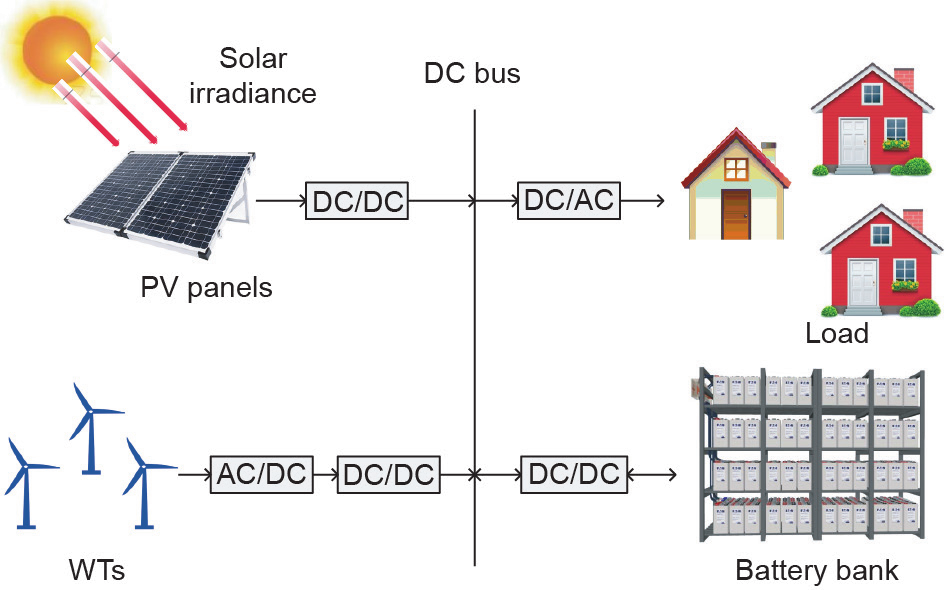
图1. 提出的HRES的系统模型。AC：交流电；DC：直流电。

RES发电有3种不同的模式：平衡、盈余和赤字。在平衡模式下，RES（包括WT和PV）产生的总功率等于总用电设备负荷，故不存在盈余或不足功率；在盈余模式下，RES产生的总能量大于用电设备的总负荷，因此使用ESS可将额外的能量储存在动力组的电池中，此时，能量从RES流向家庭和ESS；在缺电模式下，RES 产生的功率低于用户所需的功率，可利用ESS来满足用户的负载，此时，能量从RES和ESS流向用电设备的负载。因此，ESS与RES的结合使用增加了可靠性因素，并且混合模型对用户而言更加经济实惠。

《2.2. 提出模型的容量公式》

2.2. 提出模型的容量公式

本节介绍RES、ESS和TAC的建模。（1）光伏发电系统的容量公式。太阳辐射I的每小时光伏板输出功率由式（1）给出[19]：

式中，POW^pv(t )是时隙t 产生的每小时光伏板总功率，W； P_r^pv是额定光伏功率；I 代表太阳能绝缘数据，W?m^–2 ；I ^ref 表示参考条件下的太阳能绝缘，值为1000 W?m^–2 ；T ^cof 是光伏板的温度系数，对于单晶硅和多晶硅，设定为–3.7 × 10^–3 ℃^–1 [19]；T ^ref代表给定参考条件下的光伏电池温度，通常设定为 25 ℃；T ^c 代表电池温度，可通过式（2）得到：

式中，T ^amb表示环境空气温度，℃；T ^noct表示正常工作电池温度，℃，T ^noct取决于制造商对光伏组件的规格。

如果存在多个光伏板N ^pv，则总发电功率ξ ^pv可给出如下：

（2）WT电力系统的容量公式。WT发电机产生电能的机制完全基于风能。风力发电机可由两个或多个叶片组成，这些叶片机械地连接到根据风速产生动力的电机上。为了提高WT效率，涡轮机被安装在高高的塔架上。时隙t 处的WT功率通过式（4）计算[33]：

 

式中，υ 表示风速；P_r^wt表示WT的标称功率；υ ^r 、υ ^co 和υ ^ci 分别表示额定风速、切出风速和切入风速。参数x 和y 可通过式（5）获得：

如果一个区域内安装的WT数量为N^wt，则总产生的风力发电量ξ ^wt(t )可通过式（6）获得：

（3）RES累计发电量与用户负荷公式。PV和WT累计发电量ξ ^gen(t )可表示为：

式中，η_i 表示逆变器的效率。

在家庭中，用户在时隙t 的负荷ξ ^ld取决于电器的使用情况。因此，ξ ^ld可由式（8）计算：

式中，g 和p 分别表示设备的数量及其额定功率；χ (t )是显示设备状态的布尔整数，当χ (t )=1时，设备状态在时间t被认为是打开的，否则被认为是关闭的。

（4）电池组的容量确定。由于太阳辐射和风速的间歇性，电池组的储能能力会发生变化。当ξ ^gen(t )大于ξ ^ld(t )时，电池组处于荷电状态（state of charge, SOC）。因此，通过式（9）得到时隙t处电池组的充电量[19]：

式中，ξ ^store(t )和ξ ^store(t – 1)分别表示时隙t 和t – 1在电池组中的存储量；表示自放电状态；η^b 表示电池组充电效率。

当ξ ^gen(t )在时隙t 小于ξ ^ld(t )时，蓄电池组中的储能可用来满足用户的负载。此时，电池组的状态变为放电状态。假设电池组放电效率为1，且本研究不考虑温度效应。因此，时隙t 处的电池组充电量由式（10）给出：

《2.3. 电池组中电池总数的计算》

2.3. 电池组中电池总数的计算

PV-WT-电池HRES中的一个重要决策变量是计算电池组所需的电池总数（N^b ）。N^b 取决于用户的负载要求和RES的发电量。为了得到变量N^b ，假定使用一个临时存储变量（temp）并将其初始化为0。在时刻t 瞬间，当 RES的发电量高于用户的负载时，该临时存储变量按照式（9）储存能量。但是，当RES产生的发电量小于时隙t的用电负荷时，将使用式（10）更新临时存储变量。因此，得到系统电池的总数取决于变量temp的曲线。 temp的正值表示RES的发电可用性，而负值表示各个时隙中的发电不足。总所需存储容量（T ^rsc）是温度曲线中的最大值与最小值之差，可以通过式（11）得出：

式中，max (temp)和min (temp)分别表示临时存储变量曲线上的最大和最小生成点。因此，可以使用式（12）[34]得出给定系统所需的N^b 的计算式：

式中，1.35是电池的标称容量。

《2.4. 系统可靠性》

2.4. 系统可靠性

可靠性是SA系统中必须考虑的重要因素。因此，在本文中，考虑并实施了供电损失率（loss of power supply probability, LPSP）的概念以获得可靠的HRES。 LPSP由0到1范围内的数字表示。LPSP为0表示系统非常可靠，将永远满足用户的负载。LPSP为1表示永远不会满足负载。1年（T=8760 h）的LPSP可以表示为：

LOPS代表电源中断的地方。当HRES产生的总能量ξ ^gen小于任何时间段内用户的总负荷ξ ^ld时，就会发生 LOPS。LOPS的定义如式（14）所示。

图2给出了计算混合动力系统可靠性的流程图。该图针对总数量X =50给出。

《图2》

图2. 计算混合动力系统可靠性的流程图。

《2.5. TAC 的制定和约束》

2.5. TAC 的制定和约束

在本节中，将基于TAC最小化制定目标函数以及约束条件。

（1）目标函数。目标函数基于找到HRES满足最小TAC时满足用户负载所需的最佳组件数，表示为ζ ^tac。 TAC是由两种不同的成本推导而来的，即年度资本成本ζ ^cap和年度维护成本ζ ^mtn。前者成本发生在项目开始时，而后者成本发生在项目生命周期内。因此，ζ ^tac的最小化由式（15）给出：

初始资本成本需要转换为年度资本成本。为此，本文使用了资本回收因子（capital recovery factor, CRF）方法。CRF由式（16）得到[19]：

式中，i ^r 表示利率；n 表示系统的寿命（以年为单位）。

在项目生命周期中，经常要更换用于PV-WT-电池 HRES的几个组件。例如，作为组件的电池的寿命估计为5年。与参考文献[19]中使用的方法类似，通过单次付款的现值因子可以使用式（17）推导得到：

式中， 代表电池的当前价值；ρ^b 代表电池的价格。

类似地，逆变器/转换器的寿命估计为10年。因此，可以使用式（18）定义通过一次付款的现值因子：

式中，代表逆变器/转换器的当前组件价值；ρ^inv/conv 表示逆变器/转换器的价格。

通过将PV-WT-电池HRES分成PV板、WT、电池和逆变器/转换器的年成本，可获得等式（19）：

式中，ζ ^wt表示WT的单位成本；ζ ^pv表示光伏面板的单位成本；ζ ^b 是电池的单位成本；ζ ^inv/conv表示逆变器/转换器的单位成本；N^inv/conv表示逆变器/转换器的数量。

等式（20）可用于获得系统组件的年度维护成本ζ ^mtn：

式中，ζ ^pv,m和ζ ^wt,m分别表示光伏面板和WT的年度维护成本。在本文中，未考虑逆变器/转换器和电池组的维护成本。

（2）约束条件。任何时候ξ ^store(t )的电池组电荷量受式（21）给出的最小和最大存储容量约束：

式中，ξ ^{store, max}代表电池组最大充电量；ξ ^{store, max}取电池组的标称容量ξ ^store值；ξ ^{store, min}表示电池组的最小充电量，其由式（22）计算得出：

式中，DoD (depth of discharge)表示最大放电深度。

为了有一个可靠的系统，在成本最小化优化过程中考虑等式（23）中给出的LPSP约束：

式中，LPSP^max 表示允许的LPSP最大值，由用电方指定。

此外，还应满足以下对光伏电池板、WT和电池总数的限制：

式中，N^{pv, max}、N^{wt, max} 和N^{b, max} 分别表示PV面板、WT和电池的最大数量。在本文中，决策变量的最小和最大范围对于 PV面板设置为0~300，对于WT设置为0~200，对于电池为 0~20 000。表1 [19]给出了PV-WT-电池混合系统所需的组件和参数。图3提供了基于输入、处理和输出的HRES过程的示意图。

《表1》

表1 混合动力系统部件和参数

A^pv: area of the PV panel; η^pv: efficiency of the PV panel; P_r^inv/conv: rated power of invertor/convertor; η^inv/conv: efficiency of the inverter/converter.

《图3》

图3. HRES过程示意图。

《3. 求解方法》

3. 求解方法

受非算法特定技术的启发，本文使用Jaya、TLBO 和混合JLBO算法解决了最佳单元容量问题，并将结果与需要特定交叉和变异参数的GA结果进行了比较。

《3.1. Jaya》

3.1. Jaya

Jaya优化算法仅考虑公共控制参数，包括种群大小和终止标准，并且不需要任何特定于算法的参数即可执行。在Jaya算法中，目标函数在每次迭代i时都被最小化，其决策变量的数量为“c ”（j=1, 2, …, c），而候选变量的数量为“e ”规模（k=1, 2, 3, …, e）的解。选择最佳候选，它在整个解决方案中具有的最佳值。同样，的最差值由表示，它被指定为整个总体中最差的候选值。如果代表第i 次迭代中第k 个候选对象的第j 个变量的值，则根据式（27）[29]定义的标准对其进行更改：

式中，O_j,best,i 和O_j,worst,i 分别是第i 次迭代中最佳和最差候选变量j 的值；描绘了O_j,k,i 的更新值，而rand_1,j,i 和rand_2,j,i  表示第i 个变量在第i 个迭代期间的两个随机数，范围为从0到1；表达式rand_1,j,i  (O_j,best,i  – O_j,k,i  )表示解决方案向最佳解移动的倾向，而表达式rand_2,j,i  (O_j,worst,i  – O_j,k,i  )表示避免采用最差解的倾向。上述条件仅在达到更好的适应性值时才被接受。在优化过程中，采用公认的解决方案来更新下一代的总样本。为了避免出现负数和两位数的值，我们分别使用MATLAB 的绝对函数和下限函数来获取决策变量的整数值。

《3.2. 基于教与学的优化》

3.2. 基于教与学的优化

在TLBO中，人口的行和列分别代表学习者和学科。学习者的每个科目都与决策变量相关，而学习者的总科目数则对应一个解决方案。TLBO过程分为两个不同的阶段：教师阶段和学习者阶段。前一个阶段显示了向老师学习，而后一个阶段则是通过学习者之间的互动与学习相关联[30]。

在教师阶段，学习者的平均值是按学科计算的。通过适应度函数对所有学习者进行评估，并选择具有最小 TAC的最佳学习者作为教师。现在该算法尝试将学习者的平均值转移给老师。因此，将由当前和最佳均值向量形成的新向量添加到现有种群中，如式（28）所示：

式中，r 表示0到1范围内的随机数；T_factor 是教学因子（teaching factor, TF）。TF被选择为1或2。应该指出的是，T_factor 不视为输入参数，而是由算法在优化过程中以相等的概率随机决定，如式（29）所示：

而式（28）中的仅在提供更好的适应度函数值时才被接受。

在学习者阶段，每个学习者会与其他学习者随机互动，以分享和增加他们的知识。该过程开始于从现有人口中随机选择两个学习者：和，使得m ≠n 。根据学习者的适应度值，通过式（30）更新总体：

仅在达到更好的适应度功能值时才被接受。算法的优化过程一直持续到满足某些终止条件为止。

《3.3. JLBO》

3.3. JLBO

JLBO由Jaya组成，其后是TLBO的学习阶段，这使其围绕全局解决方案的搜索能力增强。图4给出了JLBO 算法优化过程的流程图。下面给出JLBO算法获得HRES 的最佳单元容量解决方案的步骤。

步骤1：输入每小时的输入参数（包括太阳辐射、风速、环境温度和消费者的负荷曲线数据）。

步骤2：根据输入数据，通过式（1）和式（4）计算单个PV面板和WT的发电量。

步骤3：随机生成大小为50的初始总体，该初始总体仅由两个决策变量组成：X=[N^pv, N^wt]。在此位置向量中，第一个元素表示PV面板的总数，第二个表示WT 的总数。为了将决策变量保持在搜索空间内，最小和最大边界（约束）必须满足式（24）和式（25）。

《图4》

图4. JLBO算法的流程图。

步骤4：在这里，我们使用式（12）计算X 的每个方案的电池数量，并应用式（26）中给出的约束更新X，使其现在代表3个整数决策参数值：X=[N^pv, N^wt, N^b ]。在此，第三个元素对应于电池的总数。这些性能参数是单元容量确定问题的决策变量。因此，现在生成的初始总体是[50×3]的矩阵，其中，50表示行，3表示每个性能参数的列。总体X 的每个对应行都描述了单元容量问题的解决方案。

步骤5：通过式（13）找到X 的每个解决方案的 LPSP。现在，仅考虑满足式（23）中给出的LPSP_max 约束的那些解决方案。

步骤6：在此步骤中，使用式（15）计算X 中每个解决方案的成本值。根据适应度函数的值，选择X 中的最佳和最差解。

步骤7：使用Jaya的式（27）更新整个X 的前两个元素（N^pv和N^wt）。

步骤8：在学习者阶段，从X 中随机选择两个解X_m 和X_n 。根据适应度函数值，通过式（30）更新X_new，使 X_new 包含更新的填充值。

步骤9：最后，重复步骤4~8，直到满足终止标准（在本研究中为100代）。

步骤10：选择基于TAC的所有代中的最佳解决方案作为最终的最佳解决方案，并返回相应的性能参数值。

《3.4. 遗传算法》

3.4. 遗传算法

遗传算法是一种受生物启发的算法，它取决于遗传评估和适者生存的概念[35]。遗传算法已通过设备调度 [36,37]和混合系统的单元容量问题[38]广泛应用于能源管理。在遗传算法中，算法的特定参数（包括选择、变异和交叉算子）在优化过程中进行初始化和调整，以实现接近最佳的全局解决方案。像其他元启发式算法一样，遗传算法过程从随机生成具有N 个数字和D 维空间的初始种群（X）开始。D 维空间中存在的基因代表问题的决策变量。在遗传算法中，染色体是由数个基因组成的完整行，形成该问题的候选解决方案。随着遗传算法优化过程的发展，所有染色体都通过适应度函数进行评估，适应度函数在本研究中为TAC最小化。在迭代过程中，最佳染色体代表局部最佳解（L_best）。

为了产生下一代的新种群（X_new），本研究应用了变异和交叉策略。在模拟中我们重复该过程，并通过适应性函数评估X_new，使用具有更好的TAC的更新解决方案用于替换以前的解决方案，直到满足终止标准。具有最低TAC的最佳解决方案被选为全球最佳（G_best）解决方案。这项研究的交叉和突变值分别设置为0.8和0.2。

《4. 模拟结果》

4. 模拟结果

本文通过使用MATLAB R2016a软件和安装2.9 GHz Intel Core i7处理器、内存为8 GB的系统获得了仿真结果，并从伊朗的拉夫桑詹获得了一年（8760 h）的日照数据（图5）、环境温度（图6）和10 m高度风速（图7）的每小时数据[39]。图5（a）至7（a）和图5（b）至7（b）分别描绘了一年中以及一年的前8 d（192 h）内的日照、环境温度和风速数据。电力消费者一年和前8 d的负荷曲线分别参见图8（a）、（b）。模拟假定电池的初始电量为其额定存储容量的30%。

《图5》

图5. 每小时的太阳辐射数据。（a）一年中；（b）一年中前8 d。

《图6》

图6. 每小时环境温度分布数据。（a）一年中；（b）一年中前8 d。

《图7》

图7. 每小时的风速分布数据。（a）一年中；（b）一年中前8 d。

《图8》

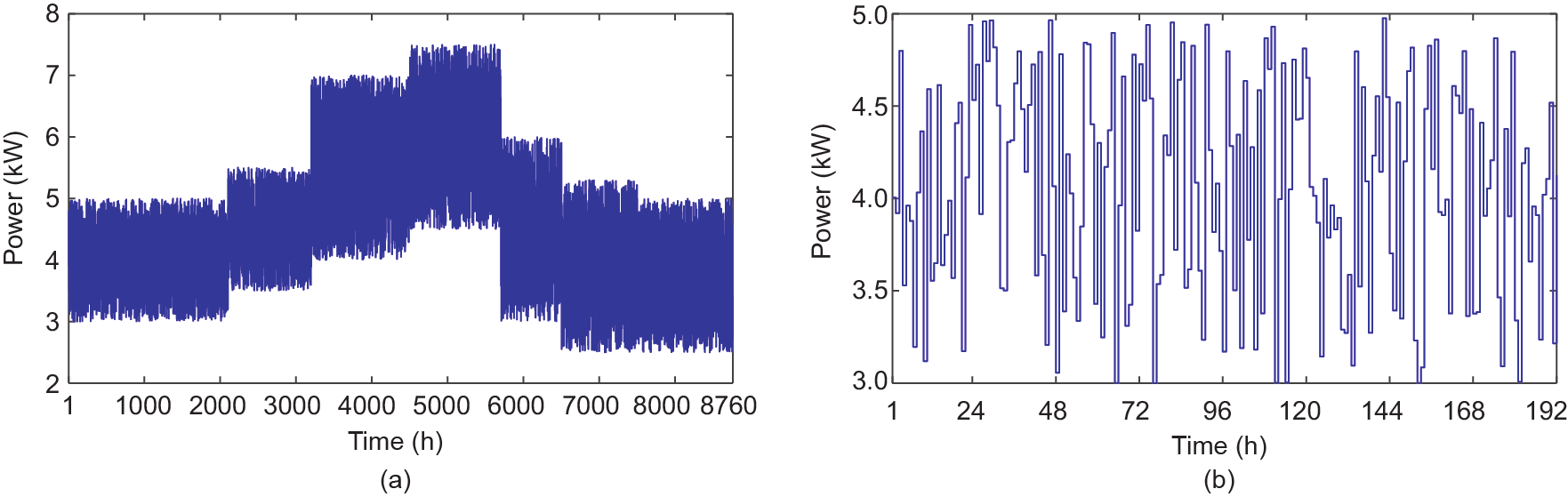
图8. 每小时用电者的负荷概况数据。（a）一年中；（b）一年中前8 d。

表2总结并阐述了通过算法获得HAC最佳容量的 TAC结果。表2给出了所有混合情况下每种算法的平均值、标准差以及最佳和最差指标。索引报告了10多次独立运行。在表2中，所提出算法的平均等级值是通过取所有3种情况（PV-WT-电池、PV-电池和WT-电池）的平均值得出的。例如，通过对PV-WT-电池、PV-电池和WT-电池案例分别获得50 247美元、67 052美元和138 250美元的平均值，可以得出JLBO的平均等级值为 85 183美元。本文基于TAC的平均等级来分配算法的各个等级。如表2所示，JLBO结果显示，在LPSP_max=1%的情况下，PV-WT-电池混合系统是最具成本效益的解决方案，TAC为50 247美元，而WT-电池和PV-电池 TAC值分别为138 250美元和67 052美元。表2中的最佳和最差指标体现了算法在10次独立运行中发现的最佳和最差解决方案。标准差表示组中的成员与组的平均值相差的数量。表2中，对于PV-电池、WT-电池和PVWT-电池的情况，JLBO在10次独立运行中获得了相同的最佳和最差解决方案。因此，其标准偏差值为0。

《表2》

表2 平均值、标准偏差（Std.）、最佳性能、最差性能汇总，以及在LPSP_max=1%时，该混合系统在独立运行10次以上的方案的排名

对于表2中列出的PV-WT-电池系统，通过Jaya算法找到的最佳指标的优化容量为N^pv=160、N^wt=9和 N^b=1296，以及50 268美元的TAC和0.9650%的LPSP。通过Jaya算法发现的最差解决方案得出的TAC为50 678 美元，优化容量为N^pv=155、N^wt=10和N^b=1306，LPSP 为0.9340%。TLBO算法找到的最佳解与Jaya获得的相同。使用TLBO算法得到的最差解实现了优化容量 N^pv=144、N^wt=13和N^b=1453，TAC为55 621美元，LPSP 为0.5859%。在混合JLBO的情况下，最佳解和最差解相同，TAC为50 247美元，优化容量为N^pv=165、N^wt=8 和N^b=1299，LPSP为0.9817%。使用GA获得的最佳指数值与使用混合JLBO获得的最佳指数值相同。使用GA 获得的最差结果是TAC为63 565美元，单元容量组合为 N^pv=115、N^wt=20、N^b=1682，LPSP为0.8211%。

对于PV-电池和WT-电池系统，所有算法均得到了相同的最佳解和最差解，因此标准偏差值为0。对于PV电池系统，最佳解和最差解的结果相同，TAC为67 052 美元，PV电池板和电池的最佳容量分别为N^pv=202和 N^b=1893，LPSP值为0.9715%。在WT-电池系统中，发现所有算法在最佳和最差情况下的结果都相似，TAC 为138 250美元，优化容量为N^wt=54和N^b=3954。在 LPSP_max=1%时，所有算法结果均为0.8744%。因此，与PV-WT-电池系统相比，由于该系统涉及的决策变量数量较少，所有算法对于PV-电池和WT-电池系统都具有相似的性能。在PV-WT-电池系统中，随着决策变量的数量增加到3个（即N^pv、N^wt和N^b ），算法的性能也随之变化。Jaya、TLBO、JLBO和GA算法在LPSP_max=1% 时的性能比较表明，在PV-WT-电池系统中，JLBO算法在均值、标准差以及最佳和最差指标方面都更好。值得注意的是，所有提出的算法都是在相同的代数中进行评估的。因此，根据算法对TAC所获得的适应性值，将其排名为JLBO、Jaya、TLBO、GA。

为简单起见，表3中仅汇总了提出的混合系统的 Jaya和JLBO算法的结果。该表提供了通过上述算法实现的根据5个不同LPSP_max处的最小TAC值，为决策变量N^pv、N^wt和N^b 提供了最佳结果。值得注意的是，与 LP-电池和WT-电池系统相比，在所有LPSP_max值下，就 TAC而言，PV-WT-电池系统都比较经济。由于增强了对解决方案空间更有希望的领域的搜索，混合JLBO在 PV-WT-电池系统中取得了更好的结果。对于PV电池和 WT电池系统，在不同的LPSP_max值下，对于所有TAC， Jaya和TLBO取得的结果都是相似的。

《表3》

表3 在不同LPSPmax值下的混合系统的Jaya和JLBO结果汇总

N/A: not applicable.

考虑Jaya算法，在LPSP_max=0时，使用145个PV电池板、15个WT和1802块电池的PV-WT-电池系统可实现TAC为66 863美元。当LPSP_max的值从0增大到5%时，相应的TAC值由于系统成本和可靠性之间的权衡而降低。换句话说，该系统更可靠，但成本更高，并且与其他LPSP_max值相比，始终可以在LPSP_max=0时满足用户的负载需求，其中LOS可能是RES产生的发电量较低所致。当LPSP_max增大至5%时，Jaya算法的PV-WT-电池系统的最小TAC值达到35 555 美元。表3的分析表明，对于Jaya算法，PV-WT-电池系统比PV-电池和WT-电池系统提供了更经济的解决方案。例如，当LPSP_max值设置为5%时，对于PV-WT-电池、PV-电池和WT-电池系统的 TAC值分别为35 555美元、39 409美元和138 250美元。

表3还显示，与Jaya算法相比，针对PV-WT-电池 HRES，JLBO算法能够获得更可观且有效的最小TAC 值结果。在LPSP_max=0时，JLBO算法获得的TAC值为 66 542 美元，比Jaya算法少321美元。在此，通过JLBO 算法找到的优化容量为N^pv=150、N^wt=14和N^b=1795。当LPSPmax值设置为0.3%时，JLBO算法获得的TAC为 60 752美元，即比Jaya算法得到的少350美元。在这种情况下，组件的最佳容量为N^pv=144、N^wt=14、N^b=1612，得到的LPSP值为0.2962%。与PV电池和WT电池系统相比，在LPSP_max=1%时，TAC值为50 247美元，且最佳容量为N^pv=165、N^wt=8和N^b=1299的PV-WT电池系统是HRES中最具成本效益的。这里，与Jaya算法相比，JLBO总共节省了21美元。此外，当LPSP_max 增大到2%时，JLBO获得的最佳容量为N^pv=168、N^wt=6和N^b=1078，TAC和LPSP分别为43 046美元和 1.7976%。在这种情况下，与Jaya算法相比，JLBO节省了20美元。最后，在LPSP_max=5%时，JLBO找到的PVWT-电池系统的TAC值为34 464美元，比Jaya算法获得的解少1091美元。此时，系统组件的最佳容量为N^pv=174、N^wt=3和N^b=818，LPSP值为4.8372%。

如表3所示，就TAC而言，通过JLBO算法获得的PV-电池系统的结果比WT电池系统更经济。在 LPSP_max=0、0.3%、1%、2%、5%时，PV-电池系统的TAC值分别为88 853美元、82 790美元、76 052美元、50 424美元和39 409 美元。对于WT-电池系统，在 LPSP_max=0、0.3%、1%、2%、5%的情况下，获得的 TAC值分别为147 730美元、142 150美元和138 250美元。接下来本文展示并讨论了用JLBO算法得到的包括RES发电量、电池组储能状态、TAC值等性能参数的仿真图及其收敛性。

用户在任何时刻负载的供能满足主要取决于RES发电量和在蓄电池组中储存的能量的范围。图9和图10分别显示了不同LPSP_max值的PV-WT-电池HRES使用PV 板和WT每小时的发电量，以及电池组在全年和一年前 8 d中的预期储能量。如图9（a）所示，最大PV功率在LPSP_max值为5%和2%时产生，N^pv分别为174和168。LPSP_max=0.3%时，PV板产生最小功率，其中，N^pv=144。在图9（b）中，由于N^wt的值均为14，WT产生的最高功率在LPSP_max值为0和0.3%时具有相似的分布。对于PV-WT-电池混合系统，当LPSP_max=5%时，WT的安装数量为3时产生最低的功率。

图9（c）和图10（c）分别展示了一年内和一年中前8 d内，在5个不同LPSP_max值下预期的电池存储能量。发现在LPSP_max=0时，由于安装了大量电池（N^b=1795）而存储了大量能量。在这种情况下，用户必须承担的最大TAC值为66 542美元。如图9（c）所示，随着 LPSP_max值的增大，由于电池数量较少，电池组中的存储能量减少。例如，当LPSP_max ＝ 0.3%、1%、2%和5%时，电池的数量N^b 分别为1612、1299、1078和818。此外，当电池中的存储能量达到最小允许极限时，会在时隙造成负载损失（loss of load, LOL）。

《图9》

图9. 在不同LPSP_max值下，一年内通过JLBO算法实现的pv-wt-电池系统每小时的发电量和储能水平。（a）产生的PV功率；（b）产生的 WT功率；（c）电池储能水平。

《图10》

图10. 在不同LPSP_max值下，一年中前8 d通过JLBO算法实现的pvwt-电池系统每小时的发电量和储能水平。（a）产生的PV功率；（b）产生的WT功率；（c）电池储能水平。

图11和图12分别显示了一年内以及一年中前8 d内，在不同LPSP_max值下每小时生产的PV-电池系统的PV功率和能量存储水平。如图11（a）所示，在LPSP_max=0时，每小时发电量最高，共有213个PV板。因此，用户承担的最高TAC为88 853美元。当LPSP_max值增大时，每小时产生的PV功率以及TAC值都会相对减小。在LPSP_max 值为0.3%、1%、2%和5%时，通过JLBO获得的PV面板数分别减少到210、202、193和187。基于此事实，PV面板产生的电量也减少了。图12（a）给出了一年中前8 d的相应PV功率。因此，取决于日照和环境温度数据曲线，PV面板的每日输出功率会相应变化。

《图11》

图11. 在不同LPSP_max值下，一年内通过JLBO算法实现的pv-电池系统每小时的发电量和储能水平。（a）产生的PV功率；（b）电池储能水平。

《图12》

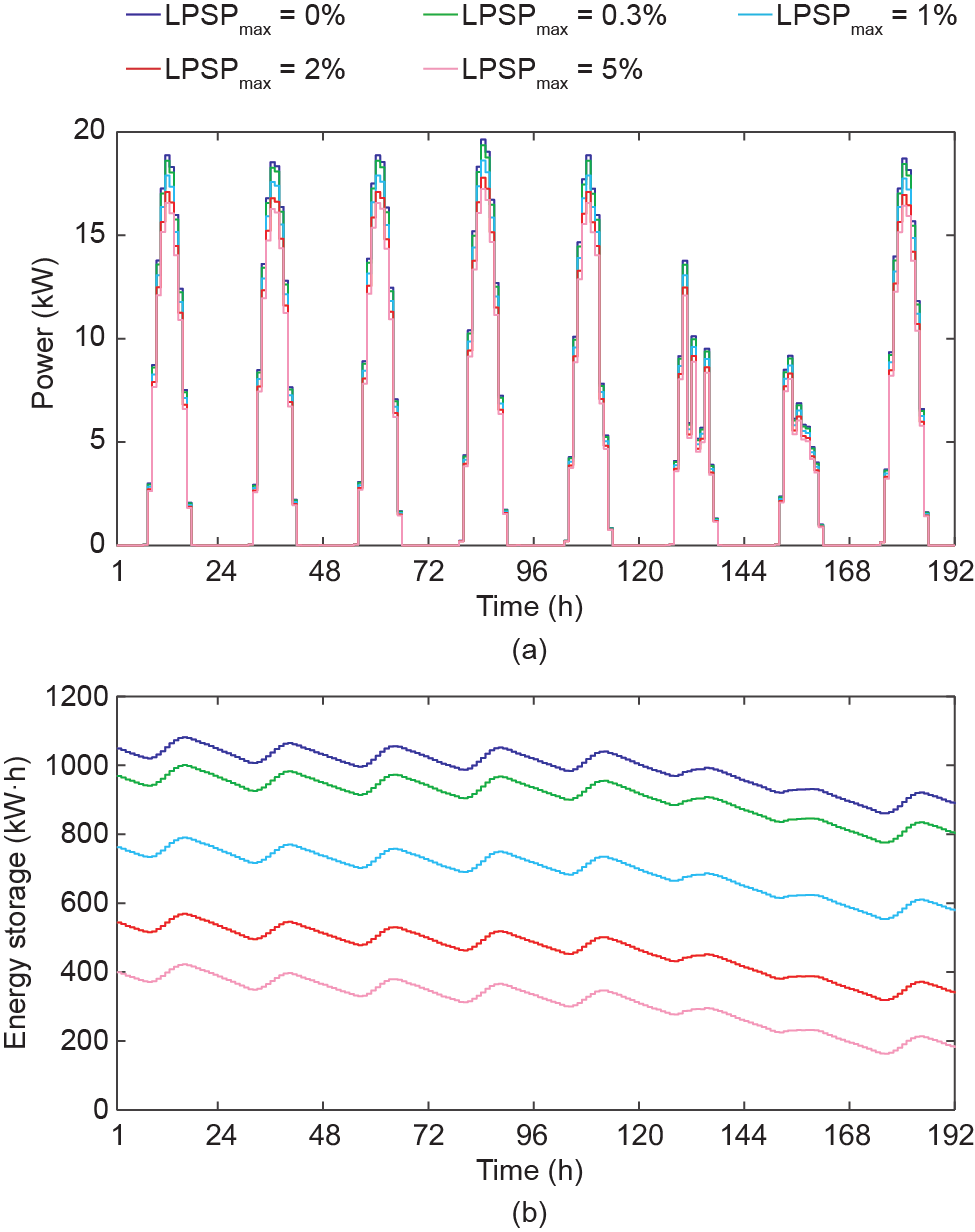
图12. 在不同LPSP_max值下，一年中的前8 d通过JLBO算法实现的pv电池系统每小时的发电量和储能水平。（a）产生的PV功率；（b）电池储能水平。

图11（b）显示了PV-电池系统的每小时电池储能水平。如前所述，假定电池初始充电量为30%。对于不同的LPSP_max，起始存储点取决于电池数量。例如，在 LPSP_max=0时，pv-电池系统的存储容量最大，N^pv=213，TAC值为88 853美元。同样，由于系统可靠性和 TAC之间的权衡效应，随着LPSP_max值的增大，存储能量的预期下降也很明显。LPSP_max为5%时，存储的能量最低，TAC值为39 409美元。图12（b）给出了一年中前8 d内不同LPSP_max对应的储能水平图。由于缺乏来自 PV板的可再生能源，PV-电池系统最初利用的是电池组存储的能量，因此图12（b）中的能量存储呈下降趋势。

图13和图14分别展示了一年内和一年中前8 d内，不同LPSP_max值下WT-电池系统每小时的发电量和储能水平。当LPSP_max=0时，WT产生的功率最高，安装的 WT数量最大，为56。当LPSP_max增大到0.3%时，N^wt降低到55，与LPSP_max=0相比，功率降低。图14（a）给出了一年中前8 d WT-电池系统在不同的LPSP_max时产生的功率。LPSP_max值分别为1%、2%和5%时，图13（a）中WT产生的功率和图13（b）中电池能量存储量的曲线与相同数量的电池和WT的曲线相似（N^b=3954，N^wt=54）。因此，对于上述三个LPSP_max值，消费者承担的 TAC相同，为138 250美元。在图14（a）、（b）中，在一年中前8 d内，WT电池系统每小时产生的WT功率和储能水平可以观察到类似的现象。

《图13》

图13. 在不同LPSP_max值下，一年内通过JLBO算法实现的wt-电池系统每小时的发电量和储能水平。（a）产生的WT功率；（b）电池储能水平。

《图14》

图14. 在不同LPSP_max值下，一年中的前8 d通过JLBO算法实现的wt电池系统每小时的发电量和储能水平。（a）产生的WT功率；（b）电池储能水平。

图15为JLBO算法下使所提出的HRES的TAC最小的收敛过程。值得注意的是，在每次迭代中，JLBO方案都会根据适应度函数降低TAC值。这证实了所提出的 JLBO方案针对最佳单元容量问题的性能和效率。还可以观察到，由于存在的决策变量较少，图15（b）和（c）所示的PV-WT-电池系统的JLBO算法的收敛过程相对于图15（a）所示的PV-WT-电池系统较快。

《图15》

图15. 在不同LPSPmax值下JLBO算法获得最优解的收敛过程。（a）PVWT-电池系统；（b）PV-电池系统；（c）WT-电池系统。

总而言之，混合算法JLBO比其他算法更具前景和成本效益。此外，因为不需要对参数进行性能调整和校准，包括Jaya和TLBO在内的非算法特定的参数方案很简单。

《5. 结论与展望》

5. 结论与展望

本文提出了非算法特有的参数方案，以寻找和评估在最小TAC值满足用户的负荷需求的HRES组件的最优容量。为了实现这一目标，本文对HRES所需的所有组件进行建模，并制定了基于TAC最小化的适应度函数。本文采用不同的LPSP_max值以保证系统的可靠性，并采用Jaya、TLBO、混合JLBO和GA算法确定了混合系统组件的最佳单元容量。在优化TAC方面，本文发现混合JLBO算法比它的前身或GA算法有更优良和经济的结果。在LPSP_max值为0、0.3%、1%、2%和5%时， TAC值分别为66 542美元、60 752美元、50 247美元、 43 046 美元和34 464美元。pv电池系统是第二经济的解决方案，wt电池系统是最不经济的解决方案。

未来，我们有意通过比较需要特定的算法参数的不同元启发式算法（包括PSO、增强差异评估、人工菌群等）来扩展后续工作。

《Compliance with ethics guidelines》

Compliance with ethics guidelines

Asif Khan and Nadeem Javaid declare that they have no conflict of interest or financial conflicts to disclose.

《Nomenclature》

Nomenclature

A^pv                     area of the PV panel

CRF                    capital recovery factor

DoD                   depth of discharge of battery

                objective function in the Jaya algorithm

           foremost value of in the entire solution

        worst value of in the entire solution

i                            number of appliances

i ^r                          interest rate

I                            solar radiation

I ^ref                       solar radiation under reference conditions

LOPS                   loss of power supply

LPSP                    loss of power supply probability

LPSP_max              maximum allowable loss of power supply probability

max(temp)         maximum generation point on the temp curve

min(temp)          minimum generation point on the temp curve

n                            life span of the system in years

N^b                         number of batteries needed for battery bank

N^b,max                  maximum number of batteries

N^inv/conv              number of the inverters/converters

N^pv                      number of PV panels

N^pv,max                maximum number of PV panels

N^wt                         number of WTs

N^wt,max                 maximum number of WTs

O_j,best,i                 Jaya best candidate values of variable j for at ith iteration

O_j,k,i                     Jaya value of jth variable for the kth candidate during the ith iteration

O_j,worst,i               Jaya worst candidate values of variable j for at ith iteration

p                          appliances power ratings

P_r^pv                        rated PV power

P_r^wt                      nominal power of WT

P_r^inv/conv              rated power of inverter/converter

POW^pv                 PV panel power output

POW^wt                 WT power

r                           random number

t                           time slot

temp                    temporary storage variable

T^amb                     ambient air temperature

T^c                          temperature of PV cell

T^cof                         PV panels temperature coefficient

T_factor                     teaching factor

T^noct                       normal operating cell temperature

T^ref                          PV cell temperature at reference conditions

T^rsc                        difference between the maximum and the minimum points in the temp curve

υ                            speed of the wind

υ ^ci                         cut-in wind speed

υ ^co                        cut-out wind speed

υ ^r                           rated wind speed

X                            total population size

                      learner m in population X

                        learner n in population X

X_new                       new population

               teacher in TLBO algorithm

ζ ^b                           unit cost of battery

                        present worth of battery

ζ ^cap                        annual capital cost

ζ ^inv/conv                unit cost of inverter/converter

              present components worth of inverter/ converter

ζ ^mtn                       annual maintenance cost

ζ ^pv                         unit cost of PV panel

ζ ^pv,m                     annual maintenance cost of the PV panels

ζ ^tac                        total annual cost

ζ ^wt                         unit cost of WT

ζ ^wt,m                      annual maintenance cost of WTs

η^b                            battery bank charging efficiency

η_i                             efficiency of the inverter

η^pv                          efficiency of the PV panel

η^inv/conv                 efficiency of the inverter/converter

                            self-discharging state

ξ ^gen                        accumulative power generation

ξ ^ld                           consumer’s load

ξ ^pv                           total produced PV power

ξ ^store                       stored amount of energy in the battery bank

ξ ^store,max                battery bank maximum charge quantity

ξ ^store,min                 battery bank minimum charge quantity

ξ ^wt                          total produced WT power

ρ^b                             battery price

ρ^inv/conv                  inverter/converter price

χ                               Boolean integer