行业新闻

怎样理解弱拓扑概念？

一个集合上的拓扑就是满足一定性质的一堆开集，按照收敛的定义，开集越多，收敛越困难。当一个集合上，原来有一个拓扑，但为了让更多的网收敛，拿掉原有拓扑中的一些开集而构成新的拓朴即可称为弱拓扑。当然，你的目的不同，有各种各样的弱拓扑。就泛函分析而言，BANACH空间上有使得有界线性泛函都连续的最弱的拓扑；BANACH空间对偶空间上有弱星拓扑；BANACH空间上全体有界线性算子全体上有弱算子拓扑，强算子拓扑。由于弱拓扑收敛性条件弱了，容易达到，会得到较原有拓扑更整齐的结论。例如，BANACH空间对偶空间的闭单位球在弱星拓扑下是紧的。

对偶空间导出弱拓扑，再导出弱星拓扑，然后再导出 alaoglu 定理

需要理解对偶空间V 与二次对偶 V** 空间，理解诱导的定义，理解拓扑基。

个人建议工科生不需要浪费时间到这些定义上，数学家为了严谨推出需要的结论，需要限定一些条件，

弱拓扑定义，注意拓扑基。

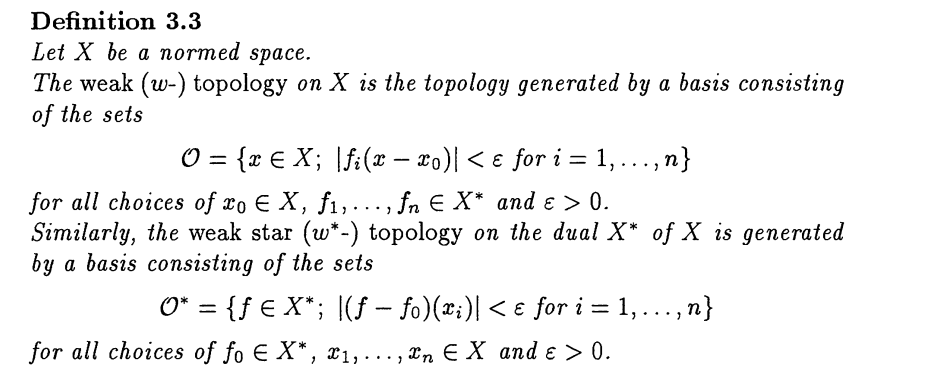
from functional_analysis_and_infinite_dimensional_geometry

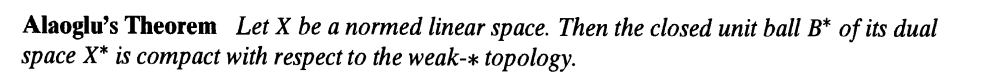
from Royden 实分析

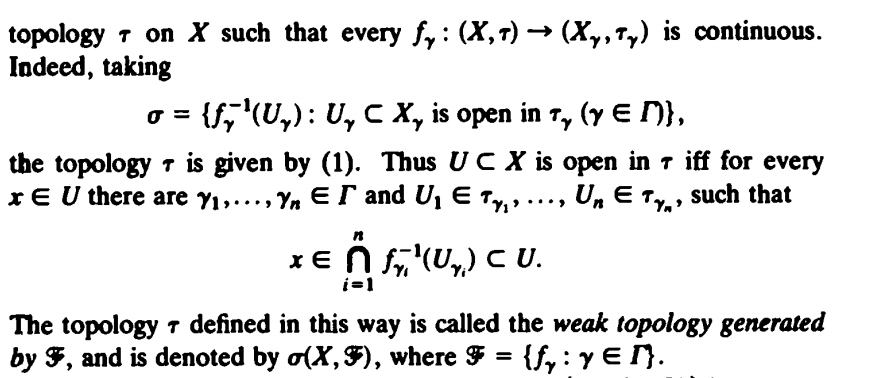
from linear analysis an introducroty course

From Fundamentals of functional analysis Douglas Farenick 这本书比较容易懂些.

恰好答主最近在看一些optimal transport的论文，在测度连续的情况下是个无穷维优化的问题，最优解在一定的情况下的存在性需要弱紧性(weak compact)保证,所以写这个回答也算复习一下泛函分析相关的一些基础知识。

什么是弱拓扑(weak topology)

简单来说，弱拓扑是使一族映射(maps)保持连续性的最“粗糙”的拓扑。我们考虑一族映射 ${（\\phi_i :X\\rightarrow Y_i)}_{i\\in I}$ 这里 ${(Y_i)}_{i\\in I}$ 为拓扑空间，X没有任何拓扑结构。我们的任务就是构造X上的最“粗糙”拓扑 $\\mathcal{J}$ ，使得每个 $\\phi_i$ 成为连续映射，这里所说的最“粗糙”的拓扑也就是弱拓扑(weak topology)。这里的最“粗糙”是指，对任意X上使得每个 $\\phi_i$ 都连续的拓扑 $\ ilde{\\mathcal{J}}$ ，有 $\\mathcal{J}\\subset \\mathcal{\ ilde{J}}$

注意到若赋予X离散拓扑(即X中每个元素都是开集(open sets))，则当然任意映射都是连续的，实际上离散拓扑是最不“经济”的一种拓扑。那么如何构造所谓的弱拓扑呢？

弱拓扑的构造

若 $\\omega_i$ 是 $Y_i$ 中的开集，那么要保证 $\\phi_i$ 的连续性，必须保证 $\\phi_i^{-1}(\\omega_i)$ 是X中的开集，也即 $\\phi_i^{-1}(\\omega_i) \\in \\mathcal{J}$ .我们遍历 $\\omega_i$ 和 $Y_i$ 得到一族集合 ${(U_\\lambda)}_{\\lambda \\in \\Lambda}$ ，当然这族集合不一定构成拓扑。于是引入下面一个问题:给定X中一个子集族 ${(U_\\lambda)}_{\\lambda \\in \\Lambda}$ ，何如构造最弱的拓扑 $\\mathcal{J}$ ，使得 ${(U_\\lambda)}_{\\lambda \\in \\Lambda}$ 中任意元素都是X中的开集。换句话，我们需要构造最“粗糙”的子集族 $\\mathcal{J}$ ，使得 $\\mathcal{J}$ 中有限个元素的交和任意多个元素的并仍属于 $\\mathcal{J}$ ，且任意的 $U_\\lambda \\in \\mathcal{J}$ .

构造分两步。第一步，通过对 ${(U_\\lambda)}_{\\lambda \\in \\Lambda}$ 有限交操作得到 $\\Phi$ ，即 $\\Phi=\\{\\cap_{\\lambda \\in \\Gamma}U_\\lambda: \\Gamma \\subset \\Lambda 是有限集\\}$ .这样得到的 $\\Phi$ 在有限交 $\\cap_{finite}$ 下是稳定的。然而 $\\Phi$ 在任意并 $\\cup_{arbitrary}$ 下不一定是稳定的，于是有第二步：对 $\\Phi$ 进行任意并的操作得到 $\\mathcal{F}$ ，即 $\\mathcal{F}=\\{\\cup_{arbitary}V:V \\in \\Phi \\}$ , 这样我们得到在任意并 $\\cup_{arbitrary}$ 下稳定的子集族 $\\mathcal{F}$ .但F在有限交下还是不是稳定的呢？如果答案是肯定的，那么我们就完成了弱拓扑的构造。由集合论，这问题的答案是肯定的，可参考例如G.Folland "Real Analysis".

总结构造基本过程： $\\{U_\\lambda\\}\\stackrel{\\cap_{finite}}\\longrightarrow \\Phi\\stackrel{\\cup_{arbitrary}}\\longrightarrow \\mathcal{F}$

在弱拓扑意义下的收敛性也叫做弱收敛(weak convergence),记为 $x_n \\rightharpoonup x$ .关于弱收敛的描述有下面一个常用的性质。

性质：设 $(x_n)$ 是X中的序列，那么 $x_n \\rightharpoonup x$ 当且仅当对任意的 $i \\in I$ , $\\phi_i(x_n)\\rightarrow \\phi(x)$ .

一般泛函分析教材对弱收敛的定义大多是直接采用这条性质。

有了这些基本的了解，我们可以更加细致地讨论Banach空间的弱拓扑。我们可以具体地写出Banach空间弱拓扑意义下的临域基，从而可以看出一般情况下强拓扑（即由Banach空间里的范数诱导的拓扑）下的开集更加“精细”，准确的说，无穷维的Banach空间，强拓扑是严格强于弱拓扑的；在有限维空间，两者是等价的。

Banach空间的弱拓扑及其对偶空间的弱*拓扑

有空再写

测度弱拓扑的引出和上面的想法差不多，测度可以在连续函数空间自然地诱导出一个函数，从而同样有弱拓扑的概念。这种观点下的弱拓扑，和测度论中测度的弱收敛是相容的，有空可以再细说。

Reference: H.Brezis, "Functional analysis, Sobolev space and Partial Differential Equation"

概念和定义其他人已经说了，我也懒得打公式，说一下weak topology和weak* topology出现的motivation吧。本质上说，这两种拓扑的引入都是为了保证某些好的性质继续得以维持。

weak topology最主要是为保证一组线性泛函continuous这一性质，为了达到这一目的，我们于是把开集数目减少，去掉不必要的开集，减少到刚好这组泛函都能保持连续。

weak* topology最主要还是为了研究compactness，毕竟这个性质太好了，我们要想办法把它留下来。但infinite dimensional情形下，original topology下的单位闭球无法保证紧性。于是乎我们引入了weak* topology来保证这点。赫赫有名的Banach-Alaoglu-Bourbaki定理说明的也正是此点。

弱拓扑是一种拉回拓扑.

[拉回拓扑]假设 $X$ 为一个集合, 而 $\\{Y_{\\alpha}\\}_{\\alpha \\in A}$ 为一族拓扑空间. 给定一族映射 $\\{\\varphi_{\\alpha}: X \\rightarrow Y_{\\alpha}\\}_{\\alpha \\in A}$ . $X$ 上使得所有 $\\{\\varphi_{\\alpha}: X \\rightarrow Y_{\\alpha}\\}_{\\alpha \\in A}$ 连续并且最粗糙的拓扑称为拉回拓扑.

[弱拓扑] 令 $X$ 为巴拿赫空间且令 $f\\in X^*$ . 我们定义线性泛函 $\\varphi_f(x):=\\langle f,x \\rangle$ , 则 $\\varphi_f:X\\rightarrow \\mathbb{R}$ . 当 $f$ 取遍 $X^*$ , 我们得到一个映射序列 $\\{ \\varphi_f(x) \\}_{f\\in X^*}$ . 弱拓扑定义为映射序列 $\\{ \\varphi_f \\}_{f\\in X^*}$ 的拉回拓扑.