公司新闻
PolarDB-X CBO 优化器技术内幕
PolarDB-X优化器是以Volcano/Cascades模型[1]作为框架的基于代价的优化器(Cost Based Optimizer),它可以为每一条SQL构造出搜索空间,并根据数据的统计信息,基数估计,算子代价模型为搜索空间中的执行机计划估算出执行所需要的代价(CPU/MEM/IO/NET),最终选出代价最小的执行计划作为SQL的具体执行方式。
PolarDB-X作为一款云原生分布式数据库,具有在线事务及分析的处理能力(HTAP)、计算存储分离、全局二级索引等重要特性,PolarDB-X优化器在这些特性中扮演了非常核心的角色。详情可以参考PolarDB-X 面向 HTAP 的 CBO 优化器。这篇文章将会为大家带来PolarDB-X CBO优化器的具体实现技术细节。
PolarDB-X优化器和大部分现代数据库优化器一样都是基于代价的优化器。它的输入为逻辑计划(通过SQL转换而成),输出是一个物理计划。核心组件包括:
- 计划空间搜索引擎(Plan Space Search Engine)
- 转换规则(Transform Rules)
- 统计信息(Statistics)
- 基数估算(Cardinality Estimation)
- 代价模型(Cost Model)
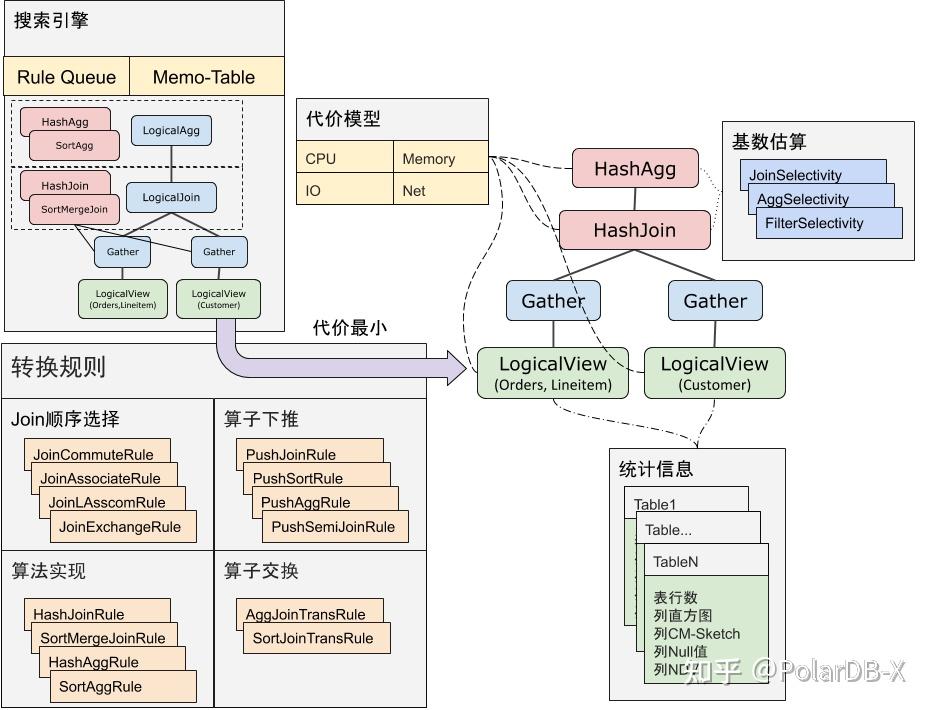
CBO 的基本优化流程:
搜索引擎利用转换规则,对输入的逻辑执行计划进行(逻辑/物理)转换,构造出执行计划的搜索空间。之后,利用代价模型对搜索空间中的每一个执行计划进行代价估算,选出代价最低的物理执行计划。而代价估算的过程离不开基数估计:它利用各个表、列的统计信息,估算出各算子的输入行数、选择率等信息,提供给算子的代价模型,从而估算出查询计划的代价。
总的来说就是利用转换规则搜索执行计划搜索空间,并评估每个执行计划代价找到最优解的过程。后面章节的结构:
- 执行计划的代价估算
- 执行计划的逻辑和物理转换
- 计划空间搜索引擎
- 实践经验分享
在展示如何找搜索执行计划之前,我们先看一下给定一个物理执行计划,我们怎么去估算它的代价。评估一个执行计划的代价需要依赖统计信息,基数估算,代价模型。
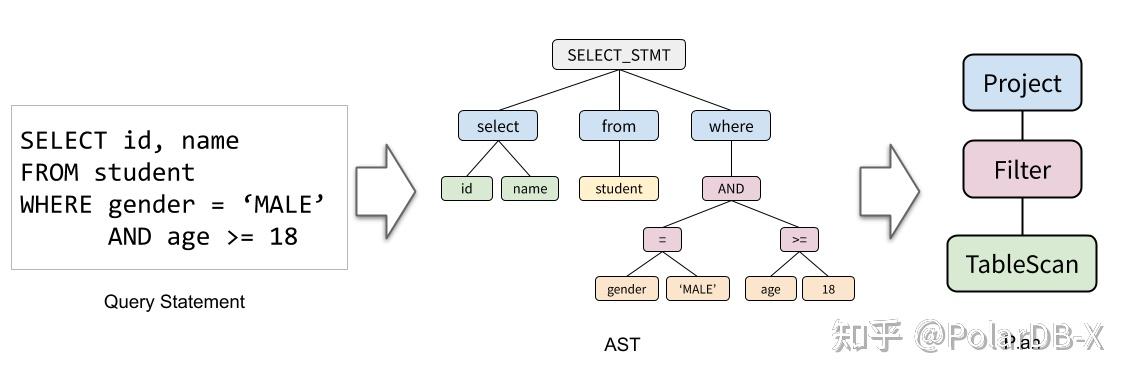
一条SQL会被Parse成抽象语法树(AST),再转成关系代数树,我们说的执行计划指的就是关系代数树。 执行计划的组成常见关系代数算子有:
- Project
- Filter
- Join (HashJoin, Index NLJoin, Partitoin Wise Join...)
- Agg (HashAgg, Sort Agg)
- TableScan
- 等等
代价模型(Cost Model)是用于估算物理执行计划的代价,PolarDB-X的代价用(CPU、Memory、IO、Net)四元组来描述。每一算子都会通过上述四元组来描述其代价,这个执行计划的代价即是其全部算子的代价的求和。最终优化器会根据求和后的CPU、Memory、IO、Net加权计算出执行计划最终的代价。
CPU:代表CPU的消耗数值
Memory:代表Memory的占用量
IO:代表磁盘的逻辑IO次数
Net:代表网络的逻辑IO次数(交互次数及传输量)
最终Cost=(CPU, Memory, IO, Net) · (w1, w2, w3, w4),W为权重向量作为例子,下面给出HashJoin、Index NLJoin和LogicalView算子(表示下推至存储计算的执行计划,内部由算子树组成)的代价计算方式,以及最终给出一个具体的物理执行计划。
HashJoin的执行代价(内存执行模式)
CPU=Probe权重 * Probe端数据量 + Build权重 * Build端数据量
Memory=Build数据量 * build端一行数据的大小Index NLJoin的执行代价(在分布式场景下,通过Batch的方式Lookup)
CPU=Outer端数据量 * Inner端Lookup一次所需CPU
Memory=BatchSize * 每Batch拉取平均数据量 * inner端一行数据的大小
IO=Outer端数据量 * Inner端Lookup一次所需IO
Net=Outer端数据量 / BatchSizeLogicalView 算子与存储交互的方式可以为SQL或执行计划,它的代价估算则是按照具体的存储特性与执行方式决定,例如:当存储为行存时,需要为LogicalView算子内的逻辑执行计划转换成行存引擎的物理执行计划,再评估代价。当存储为列存时,则需要按照列存的特定优化出对应的执行计划,再评估代价。这样就可以为不同的存储引擎评估出合理的执行计划代价。这对于计算存储分离架构的基于代价的计算下推具有重要意义,更多计算下推详情请参考PolarDB-X 中的计算下推。
LogicalView的代价=对应存储执行计划的代价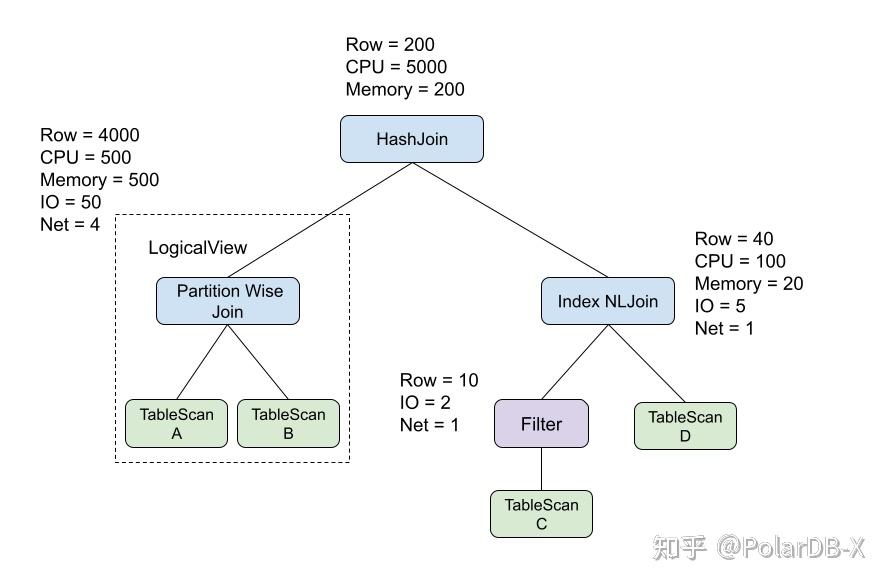
上面我们看到算子的代价计算会依赖输入算子的数据量(行数)估算,行数的估算主要通过Cardinality Estimation和Statistics来完成。对于TableScan,我们通过统计信息记录的RowCount就可以估算得比较准。而对于Filter这类过滤条件的估算需要依赖直方图,NDV(Number of Distinct Value)等信息估算Selectivity再计算算子的RowCount。
PolarDB-X的统计信息以逻辑表为单位,它包含了:
- 逻辑表的行数
- 列NDV值
- 列Null值信息
- 列等高直方图信息
当用户发起ANALYZE TABLE命令,或者是后台auto analyze线程自动发起统计信息收集的时候,PolarDB-X将会通过对逻辑表进行采样的方式收集数据并计算统计信息。
基数估计(Cardinality Estimation)会估算各个算子中间结果的行数或基数等信息,例如Join输出行数,Agg会产生的Group数量等等。
以下是几个例子:
- Join结果的行数估算 : LeftRowCount * RightRowCount / MAX(LeftCardinality, RightCardinality)
- Union结果的行数估算: LeftRowCount + RightRowCount
- Agg结果的行数估算: Group By列的Distinct值数量(NDV)
- Filter结果的行数估算: 对于等值条件,使用NDV估算选择率;对于范围查询,使用直方图估算选择率
PolarDB-X优化器的计划搜索空间的枚举是通过转换规则来完成的:
一条规则由match pattern和转换逻辑组成,搜索引擎会根据规则的match pattern在执行计划中匹配其需要的关系代数节点。按照规则的转换逻辑生成等价的执行计划。
例如:我们希望考虑每一种Join顺序的执行计划对于的代价,就需要枚举出所有对应的执行计划。 Join Reorder是通过Join的交换律、结合律等规则来实现的。
下面我们给出一条Join结合律转换规则的例子,规则匹配了两个特定顺序的Join,并将它转换成了另外一种Join顺序,这样我们就从原有的执行计划得到了一个等价的执行计划!这两个这行计划可以各自算出自己的代价并比较大小。
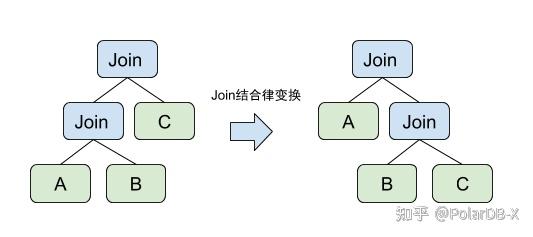
当我们加入更多的规则去枚举遍历的话,我们就可以搜索更大的搜索空间。搜索空间的控制大小在优化器中有着非常多的考量,特别是Join Reorder会产生大量等价的执行计划。搜索空间的空间大小控制问题,我们留到后面实践经验分享来讨论。
上面我们只给出了Join Reorder的转换规则例子,另外注意到Join Reorder是作用于逻辑算子树且生成逻辑算子树的,因此我们也成这类规则为逻辑转换规则,执行计划的逻辑转换就是通过一系列的逻辑转换规则来完成的。
此外还有的逻辑转换规则有:
- Agg与Join交换规则
- Sort与Join交换规则
- Join与Window交换规则
- (Join, Project, Filter, Agg)计算下推规则
- 等等
另外一类规则是物理转换规则,它的作用是将逻辑算子转换成物理算子。算子只有全部转换成物理算子以后被称为物理执行计划,并用于执行。
物理转换规则有:
- Join算子物理实现规则:HashJoin,Nested Loop Join,SortMergeJoin, Partition Wise Join
- Agg算子物理实现规则:HashAgg,SortAgg
- Sort算子物理实现规则:MemSort
- TableScan 算子物理实现规则:全局二级索引回表,全局覆盖二级索引
- 等等
有了转换规则,我们可以将执行计划进行逻辑与物理转换。但具体规则是怎么应用的、按照什么顺序去应用、怎么做得高效这是计划空间搜索引擎要处理的事情。
PolarDB-X CBO采用的是Volcano/Cascades模型的优化器,使用Top-Down的动态规划算法进行计划搜索。相比于传统以System R为代表的Bottom Up优化模型, Volcano/Cascades模型具有良好的扩展性可以较为优雅地支持像计算下推,以及Agg,Sort,Join相互Transpose的需求,具备搜索空间剪枝和物理属性驱动搜索的特性。具体实现基于开源的优化器框架Calcite,在其上增加了Duplicate Free Join Reorder和StartUpCost等特性。
由于执行计划中算子存在Reorder的可能,只考虑左深树的搜索空间下的N张表的Join顺序就有N!种。简单地暴力枚举所有可能的执行计划找到最优计划将会是阶乘级别的复杂度,因此需要动态规划来降低复杂度。将原问题递归地分解成子问题,先解决子问题、再逐步解决原问题。
动态规格的一个基本假设就是最优子结构,具体来说就是当前逻辑执行计划的最优物理执行计划=当前算子的最优执行方式 + 其输入的最优执行计划。
Best(Plan)=Best(Operator) + Σ Best(SubPlan)
以两表Join为例:Best(Plan)=Best(Join) + Best(LeftInput) + Best(RightInput)下面的讨论都是在最优子结构这一假设成立下进行的。某些算子(比如 Limit)不符合最优子结构的要求,还需要引入StartUpCost,我们留在最后实践经验分享小节中讨论。
动态规划可以通过Top-Down的从顶层算子往下逐步求解或者Bottom-Up的方式从底层算子往上求解求解。Top-Down求解相比于Bottom-Up求解的一个重要优势为搜索空间的剪枝(Branch And Bound)以及物理属性(Physical Properties)驱动搜索,介绍之前我们先了解下什么是Memo。
Volcano/Cascades模型的优化器以Top-Down方式求解动态规划,它从输入的逻辑计划开始,不断应用转换规则让计划从一个计划枚举转换至另外一个计划从而达到枚举,每次转换后得到的计划会通过Memo来确认是否已经枚举过。如果把动态规划比作“填表”的过程,这里的Memo指的就是那张“表”,每次Best(Plan)就是去Memo中看看有没有已经求解的结果,重复求解都可以在Memo中避免。
所以Volcano/Cascades模型中的Memo长什么样子呢?下面通过3张表A、B、C的Join为例子说明。
Memo是以And-Or-DAG的方式来紧凑地表达其中的所有执行计划。其中正方形代表了等价集合,圆圈代表算子(这里是Join),两者相互交替。等价集合的多个Join孩子节点代表Join都是该等价集合的一种实现方式,而Join的输入是两个等价集合。正是这样一种紧凑的形式表达了ABC三表各种不同顺序的Join方式。
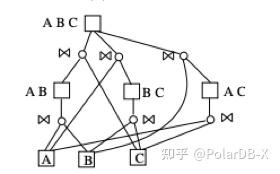
[ABC]的最优Join顺序可以通过6种组合求解。([ABC]代表A, B, C三张表的Join) 递归求解[AB]、[BC]、[AC]以此类推
ABC=[A]?[BC];[B]?[AC];[C]?[AB];[BC]?[A];[AC]?[B];[AB]?[C];
AB=[A]?[B];[B]?[A]
BC=[B]?[C];[C]?[B]
AC=[A]?[C];[C]?[A]memo的构建过程就是整个搜索空间的搜索过程。因为Memo的信息包含了所有已经搜索过的执行计划。刚开始memo为一棵简单的树只包含[ABC]、[AB]、[A]、[B]、[C]及连接它们的边,它们是通过最初的逻辑执行计划初始化生成的。后续每次规则转换都会往树上增加节点与边,例如 ([A]?[B])?[C]应用Join结合律规则得到了[A]?([B]?[C]),此时会生成[BC]来代表包含[B]和[C]的所有Join顺序。于是Memo上就会出现[BC]这样一个节点,它的输入为[B]和[C]。[A]?[BC]加入等价集合[ABC]。再经过若干次变换就会得到上面我们给出的Memo图上的形态。每次转换后的节点是否存在Memo中,通常会通过HashCode的方式检查, 如果不存在每次新转换出来的节点会继续参与转换直到不再有新的节点产生。最终得到完整的memo-table(可以获得代价最低的执行计划)
上面都是以Join为例子,实际上Memo可以有Agg,Sort,Project,Filter等其他算子。借助于Memo的执行计划空间表达形式,我们可以将不同的规则组合一起应用,产生出与传统优化器(MySQL,PostgreSQL)枚举不出来的执行计划。例如将Join, Agg, Sort, Window混合Reorder,特别是对于像PolarDB-X这样支持计算下推的存储计算分离数据库,例如Partition Wise Join将会有重大的优势。我们可以将Join Reorder与Partition Wise Join一起优化,同时考虑基于代价Join Order和计算下推的代价。
搜索引擎会按照特定的顺序去搜索计划空间,换句话来说就是我们写完转换规则,一股脑地抛给搜索引擎它将会帮我们以合理的顺序去应用规则。传统优化器如(MySQL,PostgreSQL),虽然也有基于代价的部分,但总体优化逻辑都是有多个阶段的,每个阶段按部就班地做特定优化,基本定下来以后调整就很困难,因为前后规则的依赖顺序需要人为管理。而Volcano/Cascades模型中就没有这个烦恼。
我们来思考下简单的规则应用顺序。例如:先应用逻辑转换的规则,再应用物理转换规则,很朴素合理的顺序。 但上面的顺序并不是一个最优的顺序,更好的顺序是可以进行Branch And Bound空间剪枝的顺序。
空间剪枝是Top-Down动态规划中非常棒的一个特性,它可以保证剪枝完后的空间也一定能够找到最优解。这是相对于Bottom-Up动态规划的重要优势。还是以三表Join为例子,我们来看看按照怎样的规则应用顺序可以做到空间剪枝。
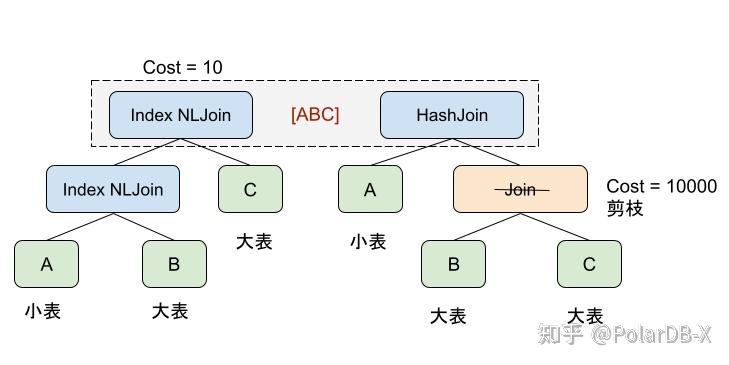
ABC的三表Join如果按照最开始的顺序优化出来了A、B、C依次使用Index Nested Loop Join,计算出代价值例如是10,之后通过Join Reorder的规则构造出了B Join C但是我们看到B Join C的最低代价也要1000, 因为是两张大表做Join,既然[ABC]等价集合中已经有了一个代价为10的执行计划。那么可以直接裁剪掉[BC]不再去为它们生成物理执行计,因为它们无论选择什么物理执行计划都不会比10低。这就是Branch And Bound空间剪枝。
这里规则的应用顺序可以看出如果从上到下应用物理转换规则那我们有机会做到剪枝,不需要去搜索部分空间。一般来说会通过特定的启发式方法来指导搜索引擎应用物理转化规则,尽快找到一个代价低的执行计划,并利用其代价去进行空间剪枝。
了解System R这类优化器这类的同学会听到一个词叫Interesting Order,它用于Bottom-Up优化过程中像SortMergeJoin,SortAgg这样需要输入有序的算子。在Bottom-Up自底向上优化的过程中,同时考虑当前算子某些可能被上层利用的顺序(Interesting Order)这样更上层的算子优化的时候,就可以利用底下算子已有的顺序。
Volcano/Cascades模型进一步拓宽了Interesting Order的概念,使其可以包含任何有物理属性意义的性质(例如:数据顺序Order,数据分布Distribution等),同时因为是Top-Down自顶向下优化过程,遇到像SortMergeJoin这类算子时候,直接要求输入具有特定的物理属性(符合Join Key的顺序)。在优化SortMergeJoin的输入算子时可以看它的等价集合中是否有满足所需顺序的物理算子,如果没有则通过Enforce Rule强制生成Sort算子保证顺序。可以看到整个物理属性的驱动方式是自顶向下的,只有上层要求底下具有某些物理属性才会被探索,这种goal-driven的方式显然更为优雅。
能看到这里的读者对优化器及其工程实践应该很感兴趣了,下面分享两个在使用Volcano/Cascades模型作为CBO优化器的框架时遇到的两个需要解决的问题。1. 基于规则的Join Reorder优化。2.StartUp Cost代价模型
PolardB-X的Join Reorder通过一系列的Join转换规则实现。计划空间搜索引擎将Join规则应用直到动态规划求解完成,此时规则对应的Join(顺序)空间也就遍历完成。可以看出一组Join Reorder规则会对应一个Join空间,而不同的Join Reorder规则对应不同的Join空间。
PolardB-X支持多种Join类型的Reorder,包括Inner/Outer/Semi/Anti Join。这些Join Reorder的规则已经有论文[3]归纳出(如下图),e代表table、a与b代表Join、p代表Join条件。下面表格主要描述了两个不同类型的Join之间可以作转换的情况(assoc、l-asscom、r-asscom)。另外还有一个只适用于Inner Join的Join交换律(comm),即左右表交换。
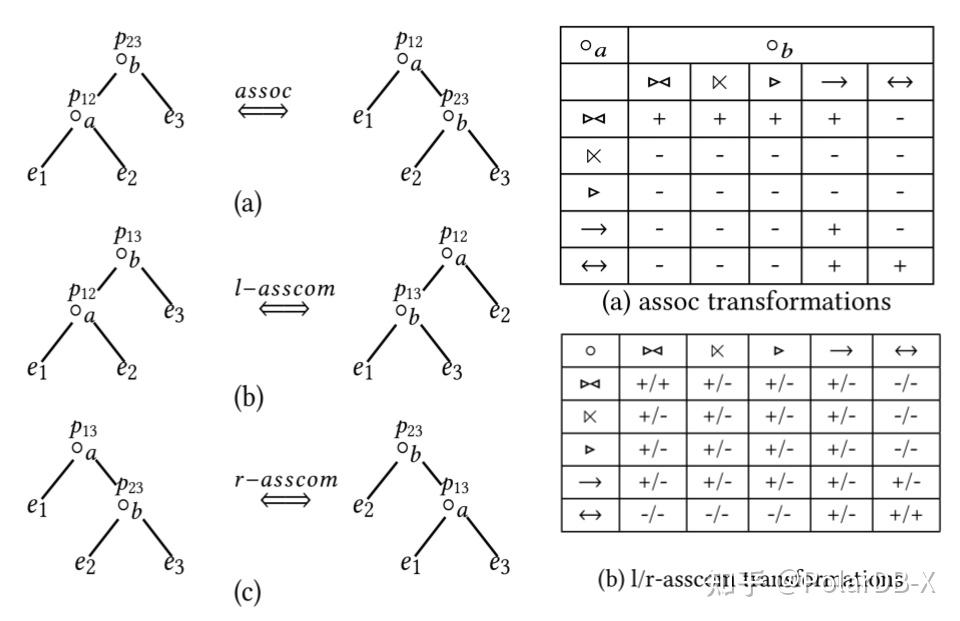
不同的规则对应不同的搜索空间:
Left Deep Tree: bottom comm规则 : A?B → B?A, 只应用于左深树的最底下两表 l-asscom规则: (A?B)?C → (A?C)?B
Zig-Zag Tree: comm规则 : A?B → B?A l-asscom规则 : (A?B)?C → (A?C)?B
Bushy Tree: comm规则 : A?B → B?A assoc: (A?B)?C → A?(B?C)
搜索空间大小:Bushy Tree > Zig-Zag Tree > Left Deep Tree
搜索空间越大或Join越多,优化搜索时间就越久,为了让优化时间维持在一定时间以内,PolardB-X采用了Adaptive Search Space,即根据Join的目决定搜索空间的大小。
| 表数目 | 搜索空间 |
|---|---|
| <=4 | Bushy Tree |
| <=6 | Zig-Zag Tree |
| <=8 | Left Deep Tree |
| >=9 | Heuristic |
下面我们思考一个问题,前面搜索引擎以Top-Down的方式求解动态规划的时候通过memo-table来避免重复计算,即每次应用规则后产生的算子树都需要到mem-table检查是否存在,如果存在则不参与后续的转换。存在的情况意味着这次的规则应用是在做无用功,我们称这种情况为generate duplicate[4]。这种重复计划的探索将会影响Join Reorder的效率,因此高效的基于规则的Join Reorder取决于对这个问题的解决。
Left Deep Tree空间对应的两条规则l-asscom与comm的就会generate duplicate,两个起始点之间存在多于一条路径。实际上Join搜索空间小节给出的Bushy Tree, Zig-Zag Tree规则都有这个问题。
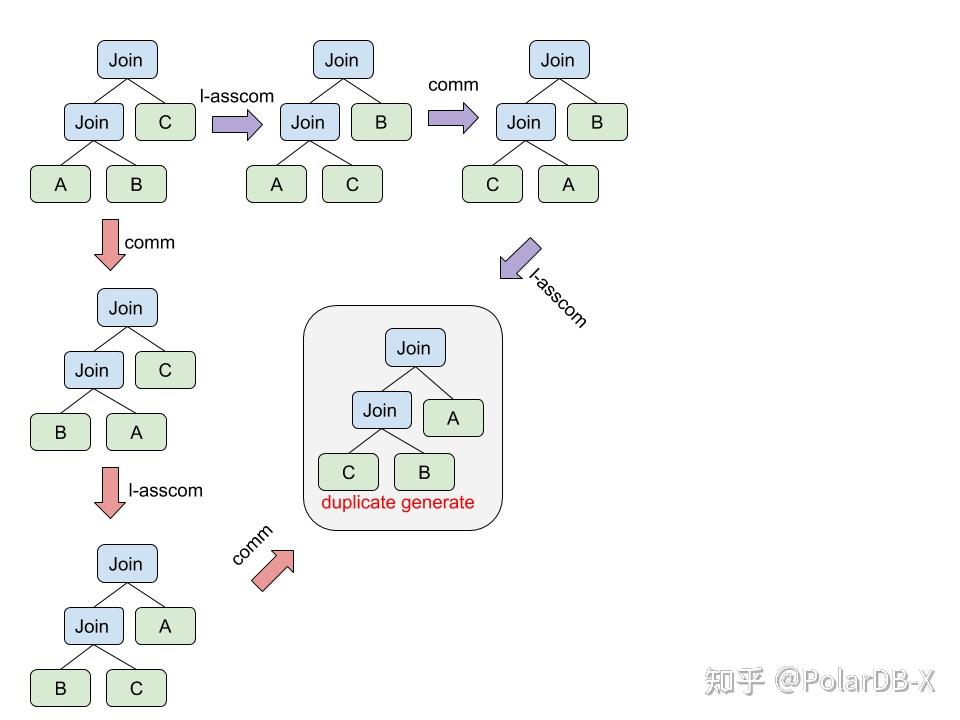
PolarDB-X为了提升优化效率会采用Duplicate-Free的Join Reorder规则[4], Duplicate-Free意味着这组规则不存在generate duplicate的情况,并且可以遍历同样完整的空间。核心思路就是通过记录算子转换的“历史路径信息”,从而避免generate duplicate
下面给出两个空间的Duplicate-Free规则
Left Deep Tree: Rule1 (l-asscom) : (A?0B)?1C → (A?2C)?3B , Rule1不能再次作用于?3 Rule2 (comm) : A?0B → B?1A,Rule2不能再以作用于?1
Bushy Tree: Rule1 (comm): A?0B → B?1A, Rule1,2,3,4均不在再次作用于?1 Rule2 (r-assoc): (A?0B)?1C → A?2(B?3C), Rule2,3,4均不在再次作用于?2 Rule3 (l-assoc): A?0(B?1C) → (A?2B)?3C , Rule2,3,4均不在再次作用于?3 Rule4 (exchange): (A?0B)?1(C?2D) → (A?3C)?4(B?5D) , Rule1,2,3,4均不在再次作用于?4
可以看见Duplicate-Free规则因为记录了“历史路径信息”导致变得复杂,“历史路径信息”实际编码在了Join算子里面,每次转换Join算子会更改对应的信息。每次规则匹配也需要检查额外条件。Zig-Zag Tree可以对Left Deep Tree的思路类似给出。
PS:上述Duplicate-Free规则转换后只考虑了Join的情况,工程实践中需要进一步考虑像Project这类优化过程中出现的算子。结果可以通过算法实现规则的应用次数(等价于csg-cmp-pair[5]数目)验证。
回忆一下最开始我们提到的Volcano/Cascades模型使用了动态规划求解,它保证能够找到最低代价的执行计划依赖了一个很重要的假设是最优子结构。其实从物理属性(Interesting Order/Physical Properties)中我们就能够隐约发现这是对最优子结构假设的调和。
下面我们来考虑更直观的SQL,当SQL带有Limit时整个最优子结构假设就不再成立,因为Join之上的Limit算子可以起到降低代价作用。整条sql希望查询的是订单表和客户表join后的10条记录。最优的执行方式显然是通过Index Nested Loop Join的方式利用索引做Join,并在返回10条结果后结束。
// orders: 1000W行
// customer: 100W行
select * from orders join customer on orders.custkey = customer.custkey limit 10PolarDB-X参考了PostgreSQL的做法为执行计划维护了StartUp Cost这样区别于Total Cost的代价。之前我们考虑的代价都是假定输入数据会全部被消费。但是Limit的出现使得数据没有被完全消费的需要。因此StartUp Cost的意义在于我返回第一条记录之前需要多少的执行代价。Hash Join的StartUp Cost就是哈希表建立所需要的代价,而Index Nested Loop Join因为利用已有的索引,所以StartUp Cost会低很多。其它算子也如此类推。
有了StartUp Cost,我们可以在Memo的等价集合中为每个等价集合维护好Best StartUp Cost的算子以及Best Total Cost的算子。在整个执行计划空间被探索后可以通过Limit算子与输入的RowCount做一个线性插值,决定选择执行计划。
Cost=StartUp Cost + fraction * (Total Cost - StartUp Cost)在我们的例子中fraction=1 / 100W。可以看见这样执行计划的代价就变更合理了。
在处理含Limit的SQL时,需要注意的是在Volcano/Cascades模型中就不能利用Branch And Bound剪枝了,因为剪枝保证了Total Cost可以找到最优解,但是StartUpCost很有可能被剪枝掉,导致最优执行计划的丢失。因此我们可以在优化前判断这个执行计划是否含有Limit来决定是否启用Branch And Bound。
PolarDB-X优化器是以Volcano/Cascades模型作为框架的基于代价的优化器,本文介绍了
- PolarDB-X 执行计划中基本的算子类型。
- 执行计划的代价是通过每一个算子的(CPU, Memory, IO, Net)四个维度进行评估的。
- 执行计划空间的枚举/遍历是通过转换规则来完成的,并且具有逻辑转换和物理转换两种类型。
- 计划空间的搜索引擎是利用Top-Down的动态规划求解出代价最低的执行计划,Memo的结构是如何高效地表达整个执行计划空间,执行计划空间是如何搜索的。
- Top-Down的动态规划求解方式相比于Bottom-Up的方式具有Branch And Bound空间剪枝和物理属性驱动搜索的优点
- 实践经验分享了Duplicate Free Join Reorder规则用于解决重复计划生成的效率问题和StartUpCost用于解决存在不满足最优子结构性质算子的问题。
[1]The Volcano Optimizer Generator
[2]On the Correct and Complete Enumeration of the Core Search Space
[3]Improving Join Reorderability with Compensation Operators
[4]The Complexity of Transformation-Based Join Enumeration
[5]Measuring the Complexity of Join Enumeration in Query Optimization
[6]Every Row Counts: Combining Sketches and Sampling for Accurate Group-By Result Estimates
[7]Apache Calcite: A Foundational Framework for Optimized Query Processing Over Heterogeneous Data Sources
[8]Orca: A Modular Query Optimizer Architecture for Big Data
[9]Efficiency in the Columbia Database Query Optimizer
开丰新闻
联系我们
公司名称: 开丰娱乐-开丰五金配件机电公司
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号

