公司新闻
Google Brain新提出的优化器“Lion”,效果要比Adam(W)更好_1
Google Brain新提出的优化器“Lion”,效果要比Adam(W)更好
- 论文地址:https://arxiv.org/abs/2302.06675
- 代码地址:https://github.com/google/automl/blob/master/lion/lion_pytorch.py
与 AdamW 和各种自适应优化器需要同时保存一阶和二阶矩相比,Lion 只需要动量,将额外的内存占用减半。 这在训练大型模型和大Batch size时很有用。 例如,AdamW 需要至少 16 个 TPU V4 芯片来训练图像大小为 224、批量大小为 4,096 的 ViT-B/16,而 Lion 只需要8个。
另一个显而易见的好处是,由于 Lion 的简单性,Lion 在我们的实验中具有更快的运行时间(step/s),通常比 AdamW 和 Adafactor 提速 2-15%,具体取决于任务、代码库和硬件。

- Lion 在 ImageNet 上从头开始训练或在 ImageNet-21K 上预训练的各种网络模型上优于 AdamW。
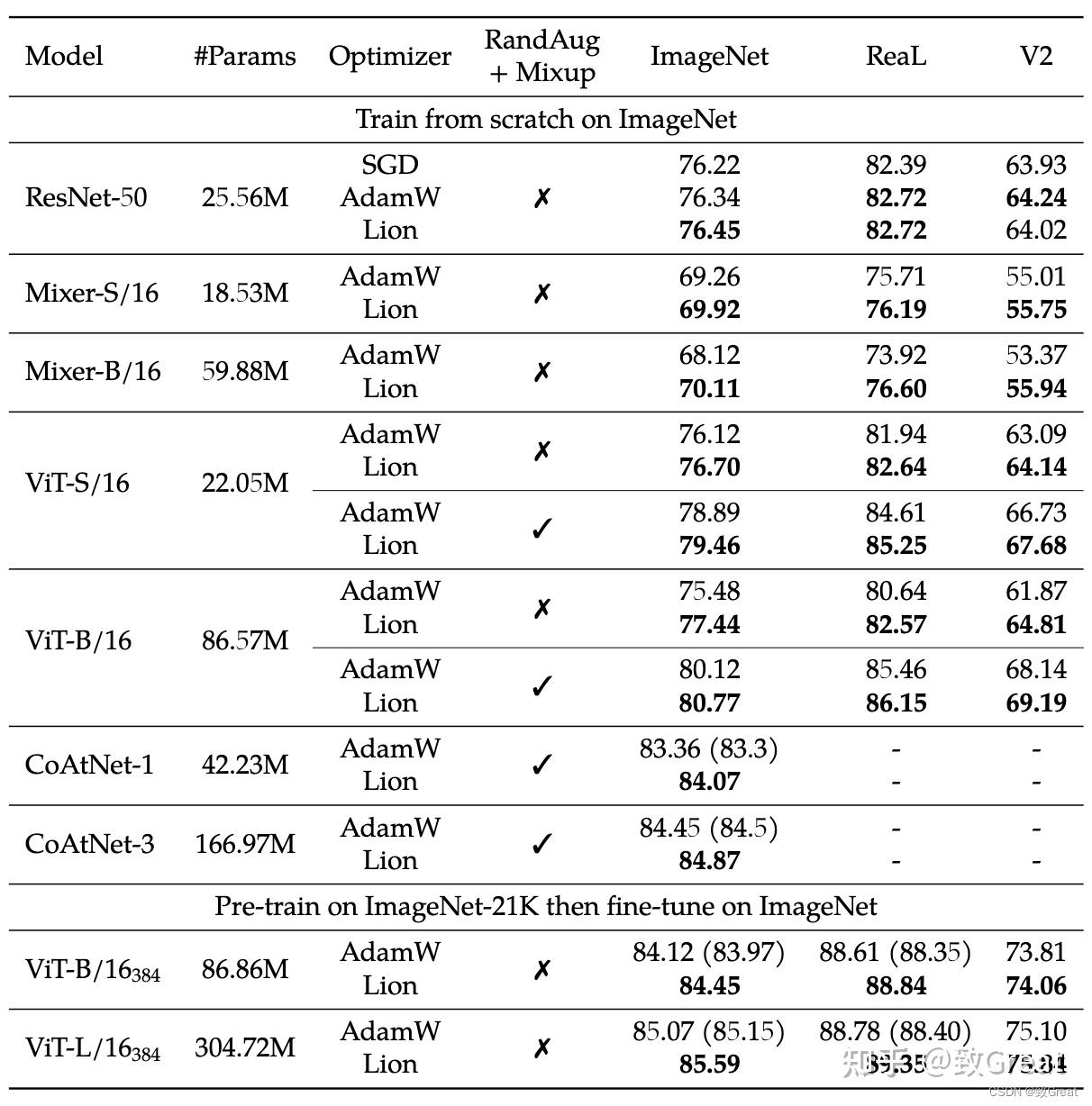
- Lion 在 JFT-300M 上节省了高达 5 倍的预训练成本。
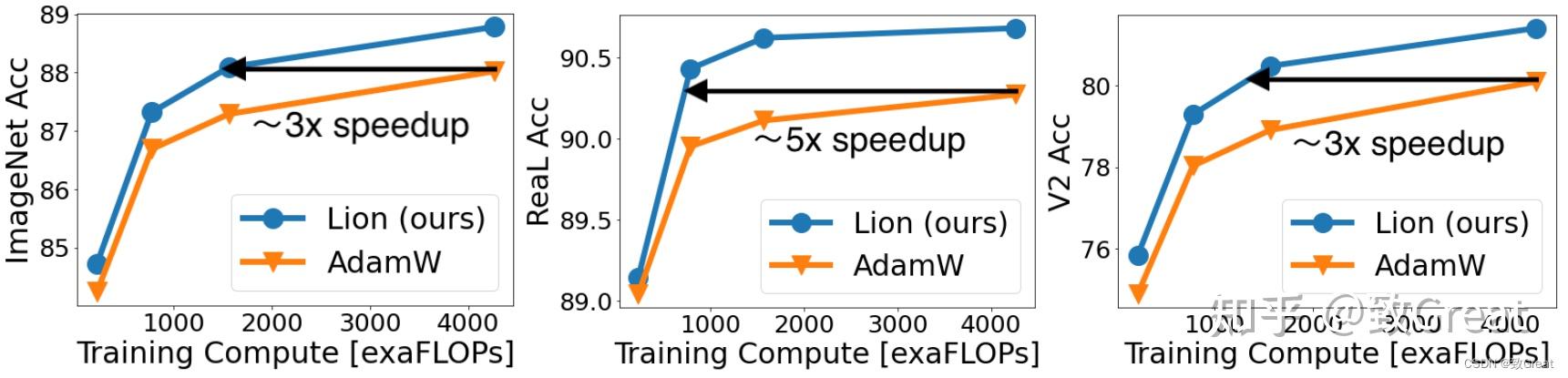
- 使用更高分辨率和 Polyak 平均进行微调后的结果。 Lion获得的 ViT-L/16 与之前由 AdamW 训练的 ViT-H/14 结果相匹配,同时缩小了 2 倍,同时对于 ViT-G/14 在 ImageNet 上进一步达到了 90.71% 的准确率。
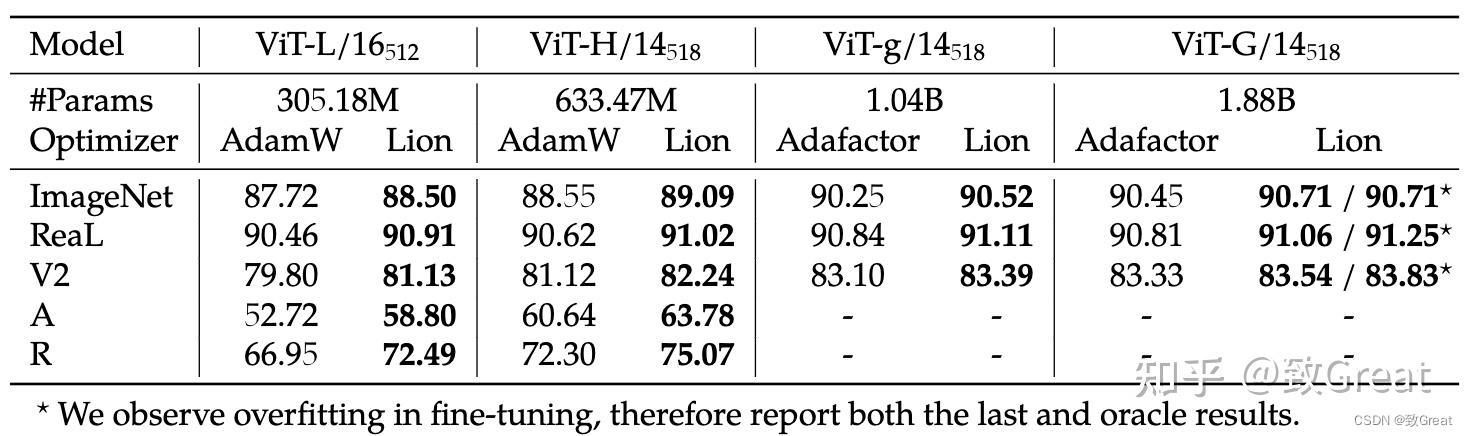
- 在 LiT 上,Lion 在零样本图像分类和图像文本检索方面击败了 AdamW。
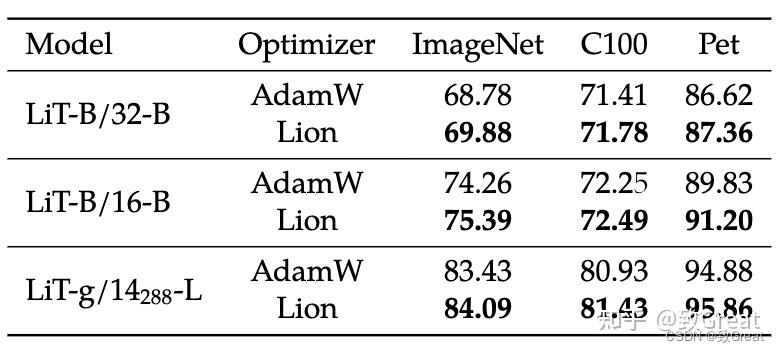
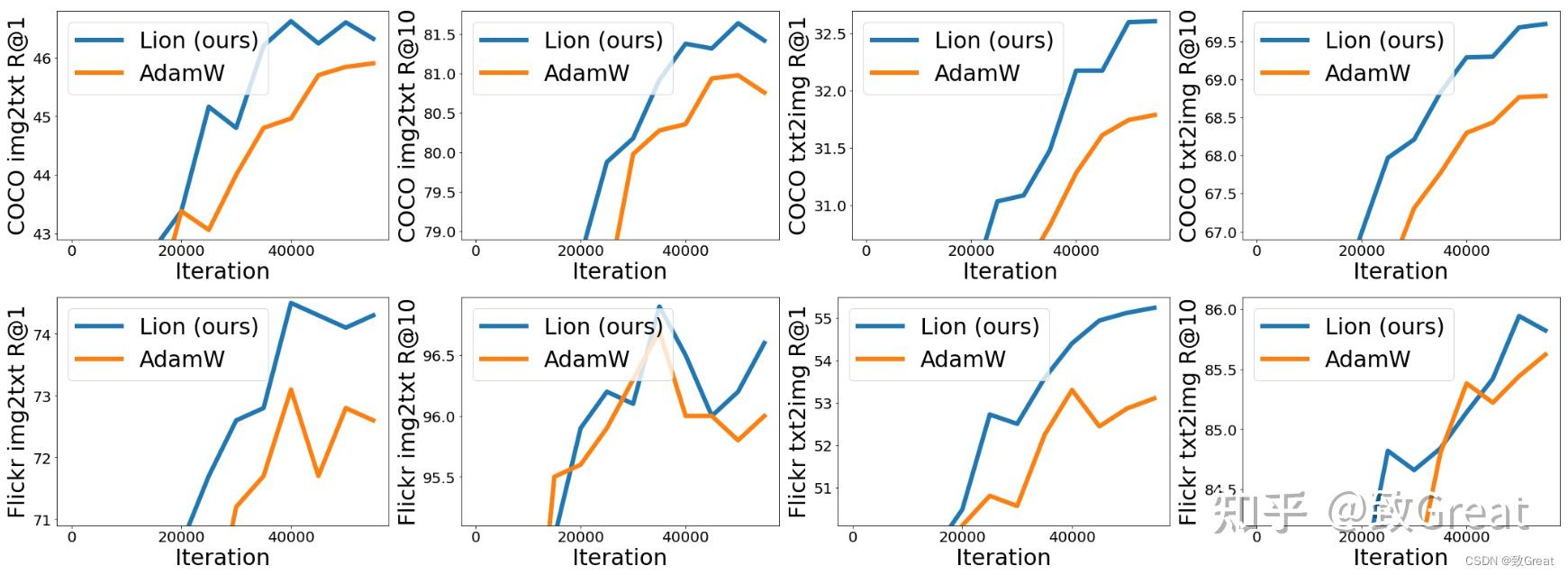
- 在 BASIC-L 上,Lion 实现了 88.3% 的零样本和 91.1% 的微调 ImageNet 准确率,分别超过之前的最佳结果 2% 和 0.1%。

- 在扩散模型上,Lion 在 FID 分数方面超过了 AdamW,节省了高达 2.3 倍的训练计算。 从左到右:在 ImageNet 上训练的 64x64、128x128、256x256 图像生成。
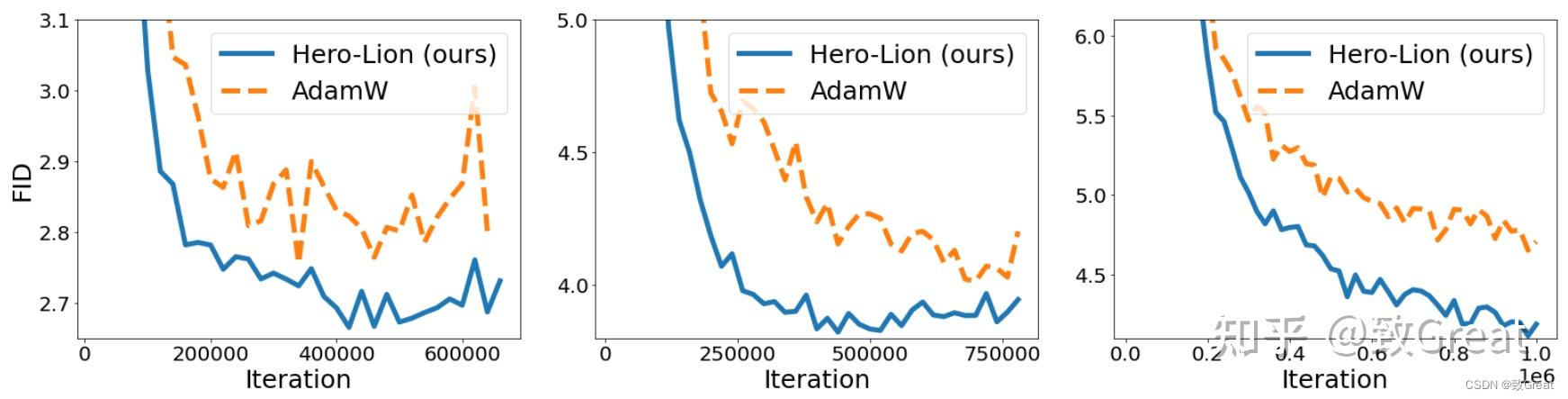
- Lion 在执行语言建模任务时在验证困惑度(perplexity)上节省了高达 2 倍的计算量(左:在 Wiki-40B 上,右:在 PG-19 上)。 Lion 在更大的transformer上获得更大的收益。
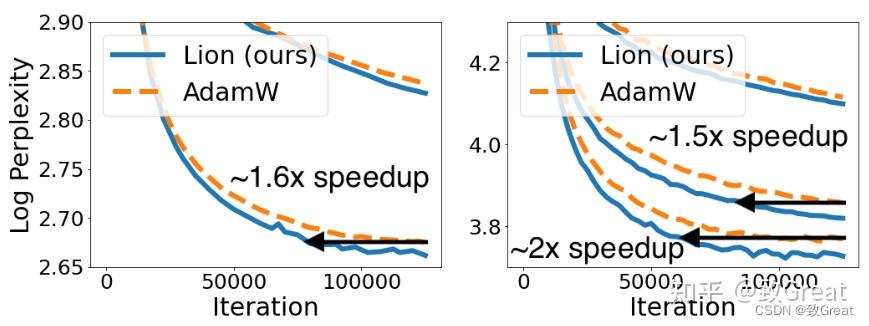
- 与 Adafactor 相比,Lion 在训练 LLM 时获得更好的平均上下文学习能力。
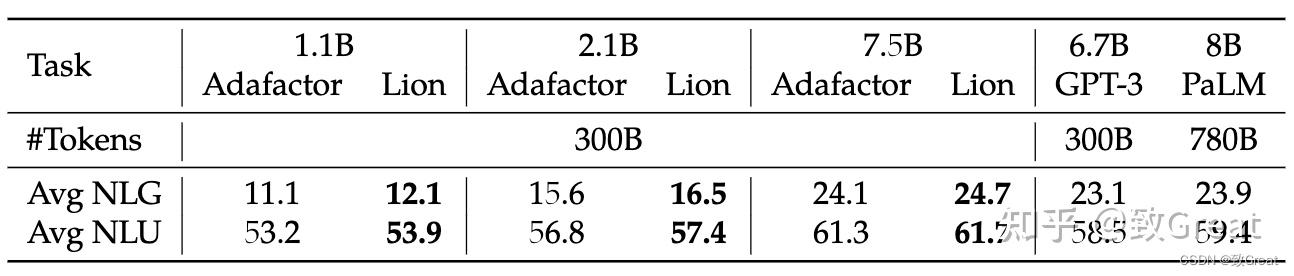
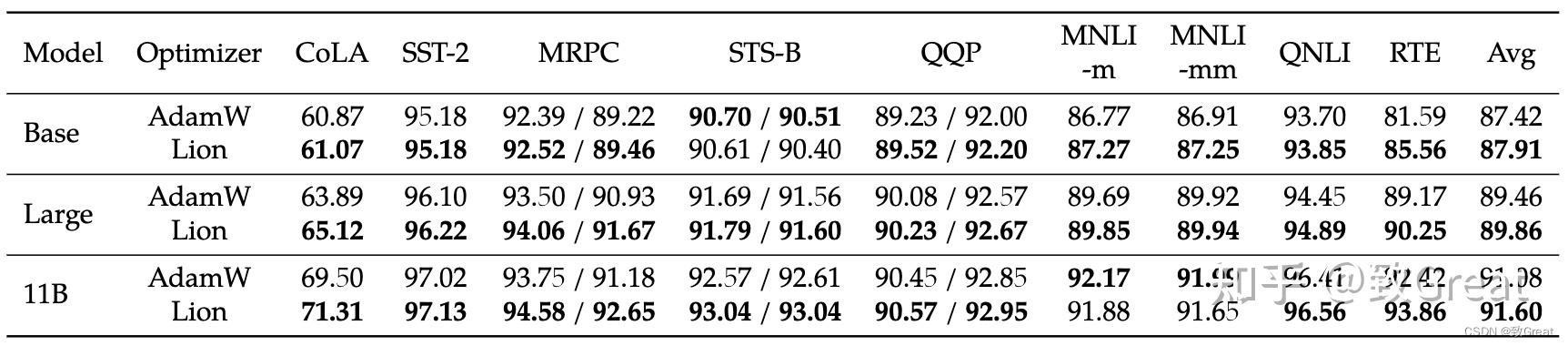
- 在 GLUE 上微调 T5 时 Lion 也更好。
- Lion 很简单,与 AdamW 和 Adafactor 相比,超参数更少,因为它不需要
和因式分解相关的参数。 为了确保公平比较,我们使用对数标度为 AdamW (Adafactor) 和我们的 Lion 调整峰值学习率
和解耦权重衰减
。 AdamW 中
和
的默认值分别设置为 0.9 和 0.999,
为
,而在 Lion 中,
和
的默认值
是通过程序搜索过程发现的,分别设置为 0.9 和 0.99。 作者只调整语言任务中的那些超参数,其中
,
在 AdamW 中,
,
在 Lion 中。 此外,AdamW 中的
设置为
而不是默认的
,因为它提高了我们实验中的稳定性,类似于 RoBERTa 中的观察结果。
- Lion 生成的更新是元素二进制
,作为符号操作的结果,因此它具有比其他优化器生成的更大的范数。 根据作者的经验,Lion 的合适学习率通常比 AdamW 小 10 倍,尽管有时小 3 倍的学习率可能表现稍好。 由于有效权重衰减为
,因此用于 Lion 的
值比 AdamW 大 10 倍,以保持相似的强度。 例如,
,
在 Lion 和
,
在 ImageNet 上训练 ViT-B/16 时使用强增强。
- Lion 中的
,
和 AdamW 中的
,
用于扩散模型。
- Lion 中的
、
和 Adafactor 中的
、
用于 7.5B 语言建模。
- 除了峰值性能外,对超参数的敏感性和调整它们的难度对于在实践中采用优化器也很关键。 在下图中,我们在 ImageNet 上从头开始训练 ViT-B/16 时同时更改
和
。 热图表明,与 AdamW 相比,Lion 对于不同的超参数选择更加稳健。
- 有些人可能会质疑 Lion 是否需要大批量大小才能准确确定方向,因为标志操作会增加噪音。 为了解决这个问题,我们使用各种批量大小在 ImageNet 上训练 ViT-B/16 模型,同时将总训练时期保持为 300,并结合 RandAug 和 Mixup 技术。 如下图所示,AdamW 的最佳批量大小为 256,而 Lion 为 4,096。 这表明 Lion 确实更喜欢更大的批处理大小,但即使使用 64 的小批处理大小,其性能仍然保持稳健。 此外,当批量大小扩大到 32K 时,只需要 11K 训练步骤, Lion 的准确率比 AdamW 高出 2.5%(77.9% 对 75.4%),证明了它在大批量训练环境中的有效性。
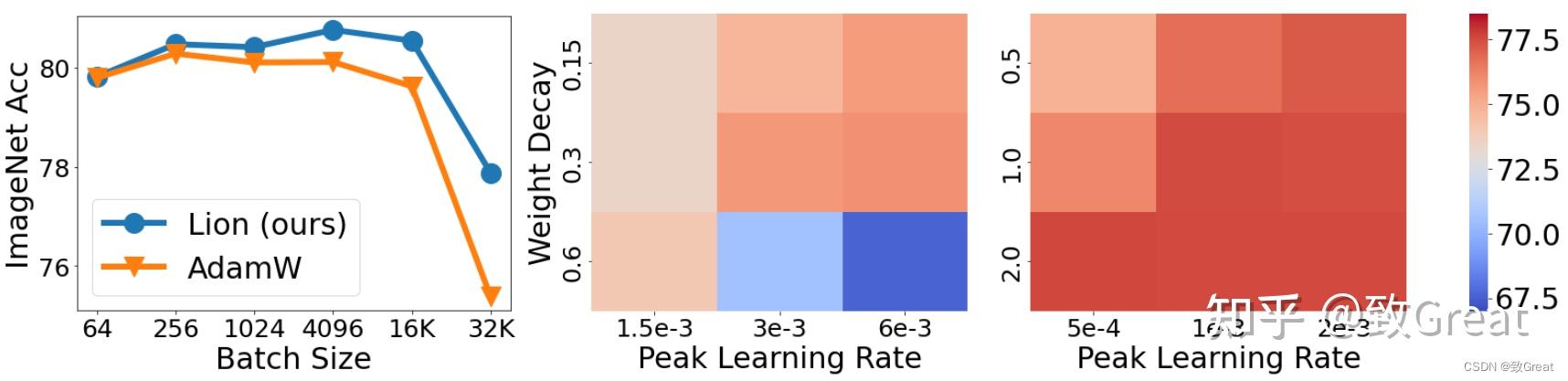
左:批量大小影响的消融实验。 Lion 比 AdamW 更喜欢更大的批次。 当我们为 AdamW(中间)和 Lion(右)改变 和
时,从头开始训练的 ViT-B/16 的 ImageNet 精度。 Lion 对于不同的超参数选择更加稳健。
"""PyTorch implementation of the Lion optimizer."""
import torch
from torch.optim.optimizer import Optimizer
class Lion(Optimizer):
r"""Implements Lion algorithm."""
def __init__(self, params, lr=1e-4, betas=(0.9, 0.99), weight_decay=0.0):
"""Initialize the hyperparameters.
Args:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
lr (float, optional): learning rate (default: 1e-4)
betas (Tuple[float, float], optional): coefficients used for computing
running averages of gradient and its square (default: (0.9, 0.99))
weight_decay (float, optional): weight decay coefficient (default: 0)
"""
if not 0.0 <=lr:
raise ValueError('Invalid learning rate:{}'.format(lr))
if not 0.0 <=betas[0]< 1.0:
raise ValueError('Invalid beta parameter at index 0:{}'.format(betas[0]))
if not 0.0 <=betas[1]< 1.0:
raise ValueError('Invalid beta parameter at index 1:{}'.format(betas[1]))
defaults=dict(lr=lr, betas=betas, weight_decay=weight_decay)
super().__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
"""Performs a single optimization step.
Args:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
Returns:
the loss.
"""
loss=None
if closure is not None:
with torch.enable_grad():
loss=closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
# Perform stepweight decay
p.data.mul_(1 - group['lr']* group['weight_decay'])
grad=p.grad
state=self.state[p]
# State initialization
if len(state)==0:
# Exponential moving average of gradient values
state['exp_avg']=torch.zeros_like(p)
exp_avg=state['exp_avg']
beta1, beta2=group['betas']
# Weight update
update=exp_avg * beta1 + grad * (1 - beta1)
p.add_(torch.sign(update), alpha=-group['lr'])
# Decay the momentum running average coefficient
exp_avg.mul_(beta2).add_(grad, alpha=1 - beta2)
return loss
开丰新闻
联系我们
公司名称: 开丰娱乐-开丰五金配件机电公司
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号

